
| A. | 1 | B. | 2 | C. | 3 | D. | 0 |
分析 (1)根据微积分基本定理,得出)∫baf(x)dx=F(b)-F(a)>0,可以看到与f(x)正负无关.
(2)注意到sinx在[0,2π]的取值符号不同,根据微积分基本运算性质,化为∫0πsinxdx+∫π2π(-sinx)dx求解,判断.
(3)根据微积分基本定理,两边分别求解,再结合F(T+T)=F(T),F(T)=F(0)判定.
解答 解:(1)由∫baf(x)dx=F(b)-F(a)>0,得F(b)>F(a),未必f(x)>0.(1)错误.
(2)∫02π|sinx|dx=∫0π|sinx|dx+∫π2π|sinx|dx=∫0πsinxdx+∫π2π(-sinx)dx=(-cosx)|0π+cosx|π2π=1-(-1)+1-(-1)=4.(2)正确.
(3)∫0Tf(x)dx=F(T)-F(0),∫T2Tf(x)dx=F(T+T)-F(T)=F(T)-F(0),则${∫}_{0}^{T}f(x)dx$=${∫}_{T}^{2T}f(x)dx$;(3)正确.
正确命题的个数为2,
故选B.
点评 本题考查微积分基本定理,微积分基本运算性质.属于基础题型.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,+∞) | B. | (-∞,0) | C. | (-1,+∞) | D. | (-∞,-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
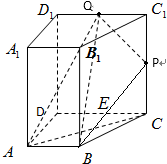 四棱柱ABCD-A1B1C1D1中,AB∥CD,CD=2,DD1=AB=1,P,Q为CC1,C1D1的中点,求证:
四棱柱ABCD-A1B1C1D1中,AB∥CD,CD=2,DD1=AB=1,P,Q为CC1,C1D1的中点,求证:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com