
分析 由题意设关于直线y=2x+m对称的点为A,B,则AB的方程为y=-$\frac{1}{2}x+n$,联立椭圆方程与直线方程,由判别式大于0求得n的范围,利用根与系数的关系求出AB的中点C的坐标,再分别代入两条直线方程,得到n与m的关系,再由n的范围求得m的范围.
解答 解:设关于直线y=2x+m对称的点为A,B,则AB的方程为y=-$\frac{1}{2}x+n$,
由$\left\{\begin{array}{l}{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\\{y=-\frac{1}{2}x+n}\end{array}\right.$,消去y整理得:4x2-4nx+4n2-12=0.
即x2-nx+(n2-3)=0.
由△=n2-4n2+12>0,得-2<n<2.
设A(x1,y1),B(x2,y2),
则${x}_{1}+{x}_{2}=n,{x}_{1}{x}_{2}={n}^{2}-3$,再设AB的中点为C(x0,y0),
则${x}_{0}=\frac{{x}_{1}+{x}_{2}}{2}=\frac{n}{2}$,
又C在y=-$\frac{1}{2}x+n$上,得${y}_{0}=\frac{3}{4}n$,
C在y=2x+m上,得$\frac{3}{4}n=2×\frac{n}{2}+m$,即n=-4m.
则-2<-2m<2,得$-\frac{1}{2}$<m<$\frac{1}{2}$.
点评 本题考查直线与椭圆位置关系的应用,考查了存在性问题的求解方法,训练了点关于线的对称点的求法,是中档题.


 初中暑期衔接系列答案
初中暑期衔接系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
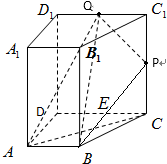 四棱柱ABCD-A1B1C1D1中,AB∥CD,CD=2,DD1=AB=1,P,Q为CC1,C1D1的中点,求证:
四棱柱ABCD-A1B1C1D1中,AB∥CD,CD=2,DD1=AB=1,P,Q为CC1,C1D1的中点,求证:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com