
【题目】某地某高中2018年的高考考生人数是2015年高考考生人数的1.5倍.为了更好地对比该校考生的升学情况,统计了该校2015和2018年高考情况,得到如下饼图:

2018年与2015年比较,下列结论正确的是( )
A. 一本达线人数减少
B. 二本达线人数增加了0.5倍
C. 艺体达线人数相同
D. 不上线的人数有所增加
【答案】D
【解析】
不妨设2015年的高考人数为100,则2018年的高考人数为150.分别根据扇形图算出2015和2018年一本、二本、艺术生上线人数以及落榜生人数,再进行比较即可.
不妨设2015年的高考人数为100,则2018年的高考人数为150.
2015年一本达线人数为28,2018年一本达线人数为36,可见一本达线人数增加了,故选项![]() 错误;
错误;
2015年二本达线人数为32,2018年二本达线人数为60,显然2018年二本达线人数不是增加了0.5倍,故选项![]() 错误;
错误;
艺体达线比例没变,但是高考人数是不相同的,所以艺体达线人数不相同,故选项![]() 错误;
错误;
2015年不上线人数为32,2018年不上线人数为42,不上线人数有所增加,选项![]() 正确. 故选D.
正确. 故选D.


科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,PA⊥平面ABCD,E为PA的中点,F为BC的中点,底面ABCD是菱形,对角线AC,BD交于点O.求证:
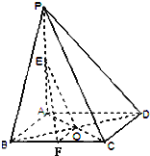
(1)平面EFO∥平面PCD;
(2)平面PAC⊥平面PBD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥P-ABCD中,底面ABCD为矩形,平面PAB⊥平面ABCD,AB=AP=3,AD=PB=2,E为线段AB上一点,且AE︰EB=7︰2,点F、G分别为线段PA、PD的中点.

(1)求证:PE⊥平面ABCD;
(2)若平面EFG将四棱锥P-ABCD分成左右两部分,求这两部分的体积之比.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆锥曲线![]() :
:  (
(![]() 为参数)和定点
为参数)和定点![]() ,
, ![]() ,
, ![]() 是此圆锥曲线
是此圆锥曲线![]() 的左、右焦点.
的左、右焦点.
(1)以原点为极点,以![]() 轴的正半轴为极轴建立极坐标系,求直线
轴的正半轴为极轴建立极坐标系,求直线![]() 的极坐标方程;
的极坐标方程;
(2)经过![]() 且与直线
且与直线![]() 垂直的直线交此圆锥曲线
垂直的直线交此圆锥曲线![]() 于
于![]() ,
, ![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三个关于x的不等式:①![]() ;②
;②![]() ;③
;③![]()
(1)分别求出①和②的解集;
(2)若同时满足①和②的x值也满足③,求m的取值范围;
(3)若同时满足③的x至少满足①和②的一个,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】请在①充分不必要条件,②必要不充分条件,③充要条件这三个条件中任选一个,补充在下面问题(2)中,若问题(2)中的实数![]() 存在,求出
存在,求出![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
已知集合![]() .
.
(1)求集合![]() ;
;
(2)若![]() 是
是![]() 成立的______条件,判断实数
成立的______条件,判断实数![]() 是否存在?
是否存在?
注:如果选择多个条件分别解答,按第一个解答计分.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com