
分析 2a1+2a2+3a3+…+nan=3n,当n≥2时,2a1+2a2+3a3+…+(n-1)an-1=3n-1,相减可得an.当n=1时,2a1=3,解得a1.
解答 解:2a1+2a2+3a3+…+nan=3n,
∴当n≥2时,2a1+2a2+3a3+…+(n-1)an-1=3n-1,
相减可得:nan=3n-3n-1=2×3n-1,
∴an=$\frac{2}{n}×{3}^{n-1}$.
当n=1时,2a1=3,解得${a}_{1}=\frac{3}{2}$.
∴${a}_{n}=\left\{\begin{array}{l}{\frac{3}{2},n=1}\\{\frac{2}{n}×{3}^{n-1},n≥2}\end{array}\right.$.
故答案为:${a}_{n}=\left\{\begin{array}{l}{\frac{3}{2},n=1}\\{\frac{2}{n}×{3}^{n-1},n≥2}\end{array}\right.$.
点评 本题考查了递推关系的应用、分类讨论方法,考查了推理能力与计算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2016-2017学年安徽豪州蒙城县一中高二上月考一数学试卷(解析版) 题型:选择题
一个等比数列的前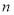 项和为45,前
项和为45,前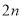 项和为60,则前
项和为60,则前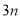 项和为( )
项和为( )
A.85 B.108 C.73 D.65
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | an=1+(n-1)lgn | B. | an=1+lgn | C. | an=1+(n-1)lg2 | D. | an=1+nlg2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | -1 | C. | -5 | D. | -5或1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com