
如图,四棱柱ABCD-A1B1C1D1的底面ABCD是正方形,O为底面中心,A1O⊥平面ABCD,AB=AA1= .
.

(1)证明:A1C⊥平面BB1D1D;
(2)求平面OCB1与平面BB1D1D的夹角θ的大小.
(1)见解析 (2)
【解析】(1)证明 法一:由题设易知OA,OB,OA1两两垂直,以O为原点建立如图所示的空间直角坐标系.

∵AB=AA1= ,
,
∴OA=OB=OA1=1,
∴A(1,0,0),B(0,1,0),C(-1,0,0),D(0,-1,0),A1(0,0,1).
由 =
= ,易得B1(-1,1,1).
,易得B1(-1,1,1).
∵ =(-1,0,-1),
=(-1,0,-1), =(0,-2,0),
=(0,-2,0), =(-1,0,1),
=(-1,0,1),
∴ ·
· =0,
=0, ·
· =0,
=0,
∴A1C⊥BD,A1C⊥BB1,
又BD∩BB1=B,A1C?平面BB1D1D,
∴A1C⊥平面BB1D1D.
法二:∵A1O⊥平面ABCD,∴A1O⊥BD.
又∵ABCD是正方形,∴BD⊥AC,∴BD⊥平面A1OC,∴BD⊥A1C.
又OA1是AC的中垂线,∴A1A=A1C= ,且AC=2,
,且AC=2,
∴AC2= +A1C2,
+A1C2,
∴△AA1C是直角三角形,∴AA1⊥A1C.
又BB1∥AA1,∴A1C⊥BB1,
∴A1C⊥平面BB1D1D.
(2)设平面OCB1的法向量n=(x,y,z).
∵ =(-1,0,0),
=(-1,0,0), =(-1,1,1),
=(-1,1,1),
∴
∴
取n=(0,1,-1),由(1)知, =(-1,0,-1)是平面BB1D1D的法向量,
=(-1,0,-1)是平面BB1D1D的法向量,
∴cos θ=|cos〈n, 〉|=
〉|= =
= .
.
又∵0≤θ≤ ,∴θ=
,∴θ= .
.


 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:高中数学 来源:2014年高考数学人教版评估检测 第九章计数原理与概率随机变量及其分布(解析版) 题型:选择题
(2014·仙桃模拟)200辆汽车经过某一雷达地区,时速频率分布直方图如图所示,则时速不低于60km/h的汽车数量为( )

A.65辆 B.76辆 C.88辆 D.95辆
查看答案和解析>>
科目:高中数学 来源:2014年高考数学人教版评估检测 第七章 立体几何(解析版) 题型:选择题
(2014·武汉模拟)如图所示,AC1是正方体的一条体对角线,点P,Q分别为其所 在棱的中点,则PQ与AC1所成的角为( )
在棱的中点,则PQ与AC1所成的角为( )

A. B.
B.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学三轮冲刺模拟 集合、常用逻辑用语、不等式、函数与导数(解析版) 题型:选择题
设函数f(x)在R上可导,其导函数为f′(x),且函数y=(1-x)f′(x)的图象如图所示,则下列结论中一定成立的是( )
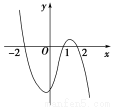
A.函数f(x)有极大值f(2)和极小值f(1)
B.函数f(x)有极大值f(-2)和极小值f(1)
C.函数f(x)有极大值f(2)和极小值f(-2)
D.函数f(x)有极大值f(-2)和极小值f(2)
查看答案和解析>>
科目:高中数学 来源:2014年高考数学三轮冲刺模拟 集合、常用逻辑用语、不等式、函数与导数(解析版) 题型:选择题
设a=log0.32,b=log0.33,c=20.3,d=0.32,则这四个数的大小关系是( )
A.a<b<c<d B.b<a<d<c
C.b<a<c<d D.d<c<a<b
查看答案和解析>>
科目:高中数学 来源:2014年高考数学三轮冲刺模拟 解析几何(解析版) 题型:选择题
设抛物线C:y2=2px(p≥0)的焦点为F,点M在C上,|MF|=5.若以MF为直径的圆过点(0,2),则C的方程为( )
A.y2=4x或y2=8x B.y2=2x或y2=8x
C.y2=4x或y2=16x D.y2=2x或y2=16x
查看答案和解析>>
科目:高中数学 来源:2014年高考数学三轮冲刺模拟 立体几何(解析版) 题型:选择题
已知正四棱锥S—ABCD中,SA=2 ,那么当该棱锥的体积最大时,它的高为( )
,那么当该棱锥的体积最大时,它的高为( )
A.1 B. C.2 D.3
C.2 D.3
查看答案和解析>>
科目:高中数学 来源:2014年高考数学三轮冲刺模拟 数列、推理与证明(解析版) 题型:选择题
已知f(x)= +log2
+log2 ,则f
,则f +f
+f +…+f
+…+f 的值为( )
的值为( )
A.1 B.2 C.2 013 D.2 014
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com