练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知正四棱锥S—ABCD中，SA＝2，那么当该棱锥的体积最大时，它的高为(　　)

    A．1　　　B.　　　C．2　　　D．3

     

    C

    【解析】如图所示，设正四棱锥高为h，底面边长为a，则a＝，即a2＝2(12－h2)，

    所以V＝×a2×h＝h(12－h2)＝－(h3－12h)，

    令f(h)＝h3－12h，则f′(h)＝3h2－12(h＞0)，

    令f′(h)＝0，则h＝2，此时f(h)有最小值，V有最大值．

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2014年高考数学人教版评估检测 第七章 立体几何（解析版） 题型：解答题

    (2014·贵阳模拟)一个几何体是由圆柱ADD1A1和三棱锥E-ABC组合而成,点A,B,C在圆O的圆周上,其正(主)视图,侧(左)视图的面积分别为10和12,如图所示,其中EA⊥平面ABC,AB⊥AC,AB=AC.AE=2.

    (1)求证：AC⊥BD.

    (2)求三棱锥E-BCD的体积.

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学三轮冲刺模拟 解析几何（解析版） 题型：解答题

    如图，四棱柱ABCD－A1B1C1D1的底面ABCD是正方形，O为底面中心，A1O⊥平面ABCD，AB＝AA1＝.

    (1)证明：A1C⊥平面BB1D1D；

    (2)求平面OCB1与平面BB1D1D的夹角θ的大小．

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学三轮冲刺模拟 解析几何（解析版） 题型：选择题

    若k，－1，b三个数成等差数列，则直线y＝kx＋b必经过定点(　　)

    A．(1，－2) B．(1,2) C．(－1,2) D．(－1，－2)

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学三轮冲刺模拟 立体几何（解析版） 题型：填空题

    三棱锥S—ABC中，∠SBA＝∠SCA＝90°，△ABC是斜边AB＝a的等腰直角三角形，则以下结论中：

    ①异面直线SB与AC所成的角为90°.

    ②直线SB⊥平面ABC；

    ③平面SBC⊥平面SAC；

    ④点C到平面SAB的距离是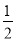a.

    其中正确结论的序号是________．

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学三轮冲刺模拟 立体几何（解析版） 题型：选择题

    设z＝x＋y，其中实数x，y满足，若z的最大值为6，则z的最小值为(　　)

    A．－3 B．－2 C．－1 D．0

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学三轮冲刺模拟 概率与统计（解析版） 题型：解答题

    如图所示，已知椭圆E经过点A(2,3)，对称轴为坐标轴，焦点F1，F2在x轴上，离心率e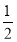＝，斜率为2的直线l过点A(2,3)．

    (1)求椭圆E的方程；

    (2)在椭圆E上是否存在关于直线l对称的相异两点？若存在，请找出；若不存在，说明理由．

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学三轮冲刺模拟 概率与统计（解析版） 题型：选择题

    已知A＝{x|x＋1＞0}，B＝{－2，－1,0,1}，则(∁RA)∩B＝( )

    A．{－2，－1} B．{－2} C．{－1,0,1} D．{0,1}

     

    查看答案和解析>>

    科目：高中数学 来源：2014年吉林省延边州高考复习质量检测理科数学试卷（解析版） 题型：解答题

    已知极坐标系的极点与直角坐标系的原点重合，极轴与直角坐标系中轴的正半轴重合，且两坐标系有相同的长度单位，圆C的参数方程为（为参数），点Q的极坐标为。

    （1）化圆C的参数方程为极坐标方程；

    （2）直线过点Q且与圆C交于M，N两点，求当弦MN的长度为最小时，直线的直角坐标方程。

     

    查看答案和解析>>

    同步练习册答案