三棱锥S—ABC中，∠SBA＝∠SCA＝90°，△ABC是斜边AB＝a的等腰直角三角形，则以下结论中：
①异面直线SB与AC所成的角为90°.
②直线SB⊥平面ABC；
③平面SBC⊥平面SAC；
④点C到平面SAB的距离是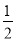
a.
其中正确结论的序号是________．
科目：高中数学 来源：2014年高考数学人教版评估检测 第三章 三角函数、解三角形（解析版） 题型：选择题
给出下列命题：
①第二象限角大于第一象限角;
②三角形的内角是第一象限角或第二象限角;
③不论用角度制还是用弧度制度量一个角,它们与扇形所对半径的大小无关;
④若sinα=sinβ,则α与β的终边相同;
⑤若cosθ<0,则θ是第二或第三象限的角.
其中正确命题的个数是( )
A.1 B.2 C.3 D.4
查看答案和解析>>
科目：高中数学 来源：2014年高考数学三轮冲刺模拟 集合、常用逻辑用语、不等式、函数与导数（解析版） 题型：选择题
设a＝log0.32，b＝log0.33，c＝20.3，d＝0.32，则这四个数的大小关系是( )
A．a＜b＜c＜d B．b＜a＜d＜c
C．b＜a＜c＜d D．d＜c＜a＜b
查看答案和解析>>
科目：高中数学 来源：2014年高考数学三轮冲刺模拟 解析几何（解析版） 题型：选择题
设抛物线C：y2＝2px(p≥0)的焦点为F，点M在C上，|MF|＝5.若以MF为直径的圆过点(0,2)，则C的方程为( )
A．y2＝4x或y2＝8x B．y2＝2x或y2＝8x
C．y2＝4x或y2＝16x D．y2＝2x或y2＝16x
查看答案和解析>>
科目：高中数学 来源：2014年高考数学三轮冲刺模拟 立体几何（解析版） 题型：解答题
如图所示，PA⊥平面ABC，点C在以AB为直径的⊙O上，∠CBA＝30°，PA＝AB＝2，点E为线段PB的中点，点M在弧AB上，且OM∥AC.
(1)求证：平面MOE∥平面PAC.
(2)求证：平面PAC⊥平面PCB.
(3)设二面角M—BP—C的大小为θ，求cos θ的值．
查看答案和解析>>
科目：高中数学 来源：2014年高考数学三轮冲刺模拟 立体几何（解析版） 题型：选择题
已知正四棱锥S—ABCD中，SA＝2
，那么当该棱锥的体积最大时，它的高为( )
A．1 B.
C．2 D．3
查看答案和解析>>
科目：高中数学 来源：2014年高考数学三轮冲刺模拟 立体几何（解析版） 题型：选择题
在正四面体P－ABC中，D，E，F分别是AB，BC，CA的中点，下面四个结论中不成立的( )
A．BC∥平面PDF
B．DF⊥平面PAE
C．平面PDE⊥平面ABC
D．平面PAE⊥平面ABC
查看答案和解析>>
科目：高中数学 来源：2014年高考数学三轮冲刺模拟 概率与统计（解析版） 题型：选择题
如图所示的是甲、乙两人在5次综合测评中成绩的茎叶图，其中一个数字被污损，则甲的平均成绩超过乙的平均成绩的概率为( )
A．
B．
C．
D．
查看答案和解析>>
科目：高中数学 来源：2014年高考数学三轮冲刺模拟 三角函数、解三角形与平面向量（解析版） 题型：选择题
命题“对任意x∈R，都有x2≥0”的否定为( )
A．对任意x∈R，都有x2<0
B．不存在x∈R，使得x2<0
C．存在x0∈R，使得x02≥0
D．存在x0∈R，使得x02<0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
a，④正确．
