练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设函数f(x)在R上可导，其导函数为f′(x)，且函数y＝(1－x)f′(x)的图象如图所示，则下列结论中一定成立的是( )

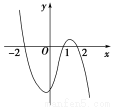
    A．函数f(x)有极大值f(2)和极小值f(1)

    B．函数f(x)有极大值f(－2)和极小值f(1)

    C．函数f(x)有极大值f(2)和极小值f(－2)

    D．函数f(x)有极大值f(－2)和极小值f(2)

     

    D

    【解析】当x＜－2时，y＝(1－x)f′(x)＞0，

    得f′(x)＞0；

    当－2＜x＜1时，y＝(1－x)f′(x)＜0，得f′(x)＜0；

    当1＜x＜2时，y＝(1－x)f′(x)＞0，得f′(x)＜0；

    当x＞2时，y＝(1－x)f′(x)＜0，得f′(x)＞0，

    ∴f(x)在(－∞，－2)上是增函数，在(－2,1)上是减函数，在(1,2)上是减函数，在(2，＋∞)上是增函数，

    ∴函数f(x)有极大值f(－2)和极小值f(2)．

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2014年高考数学人教版评估检测 第九章计数原理与概率随机变量及其分布（解析版） 题型：解答题

    (2014·郑州模拟)某学生对其30位亲属的饮食习惯进行了一次调查,并用茎叶图表示30人的饮食指数.说明：如图中饮食指数低于70的人,饮食以蔬菜为主;饮食指数高于70的人,饮食以肉类为主.

    (1)根据茎叶图,帮助这位同学说明其亲属30人的饮食习惯.

    (2)根据以上数据完成2×2列联表：

     

    主食蔬菜

    主食肉类

    总计

    50岁以下

     

     

     

    50岁以上

     

     

     

    总计

     

     

     

    (3)能否在犯错误的概率不超过0.01的前提下认为其亲属的饮食习惯与年龄有关,并写出简要分析.

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学人教版评估检测 第七章 立体几何（解析版） 题型：解答题

    (2014·贵阳模拟)一个几何体是由圆柱ADD1A1和三棱锥E-ABC组合而成,点A,B,C在圆O的圆周上,其正(主)视图,侧(左)视图的面积分别为10和12,如图所示,其中EA⊥平面ABC,AB⊥AC,AB=AC.AE=2.

    (1)求证：AC⊥BD.

    (2)求三棱锥E-BCD的体积.

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学人教版评估检测 第七章 立体几何（解析版） 题型：选择题

    (2014·黄冈模拟)设a,b是平面α内两条不同的直线,l是平面α外的一条直线,则“l⊥a,l⊥b”是“l⊥α”的( )

    A.充要条件 B.充分不必要条件

    C.必要不充分条件 D.既不充分也不必要条件

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学三轮冲刺模拟 集合、常用逻辑用语、不等式、函数与导数（解析版） 题型：填空题

    已知函数f(x)的导数f′(x)＝a(x＋1)(x－a)，若f(x)在x＝a处取得极大值，则a的取值范围是________．

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学三轮冲刺模拟 集合、常用逻辑用语、不等式、函数与导数（解析版） 题型：选择题

    设变量x，y满足约束条件，则目标函数z＝2x＋3y＋1的最大值为( )

    A．11 B．10 C．9 D．8.5

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学三轮冲刺模拟 解析几何（解析版） 题型：解答题

    如图，四棱柱ABCD－A1B1C1D1的底面ABCD是正方形，O为底面中心，A1O⊥平面ABCD，AB＝AA1＝.

    (1)证明：A1C⊥平面BB1D1D；

    (2)求平面OCB1与平面BB1D1D的夹角θ的大小．

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学三轮冲刺模拟 解析几何（解析版） 题型：选择题

    若k，－1，b三个数成等差数列，则直线y＝kx＋b必经过定点(　　)

    A．(1，－2) B．(1,2) C．(－1,2) D．(－1，－2)

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学三轮冲刺模拟 概率与统计（解析版） 题型：选择题

    已知A＝{x|x＋1＞0}，B＝{－2，－1,0,1}，则(∁RA)∩B＝( )

    A．{－2，－1} B．{－2} C．{－1,0,1} D．{0,1}

     

    查看答案和解析>>

    同步练习册答案