
分析 $\frac{C{D}^{4}+A{B}^{4}}{C{A}^{4}+C{B}^{4}}$=$\frac{C{D}^{4}+A{B}^{4}}{(C{A}^{2}+C{B}^{2})^{2}-2C{A}^{2}•C{B}^{2}}$=$\frac{C{D}^{2}+A{B}^{2}}{A{B}^{4}-2C{D}^{2}•A{B}^{2}}$=$\frac{(\frac{CD}{AB})^{2}+1}{1-2(\frac{CD}{AB})^{2}}$,设$\frac{CD}{AB}$=x>0,可得$\frac{C{D}^{4}+A{B}^{4}}{C{A}^{4}+C{B}^{4}}$=$\frac{{x}^{4}+1}{1-2{x}^{2}}$,令1-2x2=t,$\frac{CD}{AB}$=$\frac{CA}{AB}•\frac{CB}{AB}$=sinAcosA=$\frac{1}{2}$sin2A=x,可得$0<x<\frac{1}{2}$.通过换元利用导数研究函数的单调性即可得出.
解答 解:$\frac{C{D}^{4}+A{B}^{4}}{C{A}^{4}+C{B}^{4}}$=$\frac{C{D}^{4}+A{B}^{4}}{(C{A}^{2}+C{B}^{2})^{2}-2C{A}^{2}•C{B}^{2}}$=$\frac{C{D}^{2}+A{B}^{2}}{A{B}^{4}-2C{D}^{2}•A{B}^{2}}$=$\frac{(\frac{CD}{AB})^{2}+1}{1-2(\frac{CD}{AB})^{2}}$,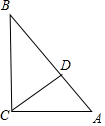
设$\frac{CD}{AB}$=x>0,
则$\frac{C{D}^{4}+A{B}^{4}}{C{A}^{4}+C{B}^{4}}$=$\frac{{x}^{4}+1}{1-2{x}^{2}}$,
令1-2x2=t,$\frac{CD}{AB}$=$\frac{CA}{AB}•\frac{CB}{AB}$=sinAcosA=$\frac{1}{2}$sin2A=x>0,∴$0<x<\frac{1}{2}$.
令1-2x2=t∈$(\frac{1}{2},1)$,则x2=$\frac{1-t}{2}$,
∴$\frac{C{D}^{4}+A{B}^{4}}{C{A}^{4}+C{B}^{4}}$=$\frac{{x}^{4}+1}{1-2{x}^{2}}$=$\frac{(\frac{1-t}{2})^{2}+1}{t}$=$\frac{{t}^{2}-2t+5}{4t}$=$\frac{1}{4}(t+\frac{5}{t}-2)$,
令f(t)=t+$\frac{5}{t}$,t∈$(\frac{1}{2},1)$,则f′(t)=1-$\frac{5}{{t}^{2}}$<0,因此函数f(t)在t∈$(\frac{1}{2},1)$上单调递减,
∴f(t)∈(6,$\frac{21}{2}$),
∴$\frac{C{D}^{4}+A{B}^{4}}{C{A}^{4}+C{B}^{4}}$=$\frac{1}{4}(t+\frac{5}{t}-2)$∈$(1,\frac{17}{8})$.
故答案为:$(1,\frac{17}{8})$.
点评 本题考查了直角三角形的边角关系、勾股定理、三角形面积计算公式、利用导数研究函数的单调性,考查了推理能力与计算能力,属于难题.


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | (1.25,1.5) | B. | (1,1.25) | C. | (1.5,2) | D. | 不能确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 等腰三角形 | B. | 锐角三角形 | C. | 直角三角形 | D. | 钝角三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 1 | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com