Question

4．将图①所示的直角梯形ABEF（图中数字表示对应线段的长度）沿直线CD折成直二面角，连接部分线段后围成空间几何体ABCDFE，如图②所示．
（I）证明BE∥平面ADF；
（Ⅱ）求空间几何体ABCDFE的表面积．

Answer 1

分析 （I）取PD的中点N，连接EN，证明BE∥AN，即可证明BE∥平面ADF；
（Ⅱ）空间几何体ABCDFE中，分别求出几个面的面积，再求面积和即可．

解答 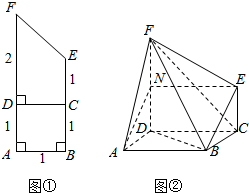解：（I）证明：取PD的中点N，连接EN，
∵EC⊥CD，ND⊥CD，CE=DN，∴四边形CDNE为正方形，
∴EN∥CD∥AB，EN=CD=AB                            
∴四变形ABNE为平行四边形，∴BE∥AN，∵AN?平面ADF，
∴BE∥平面ADF；
（Ⅱ）空间几何体ABCDFE中，S_{正方形ABCD}=1×1=1，
S_{直角梯形DCEF}=$\frac{1}{2}$×（1+2）×1=$\frac{3}{2}$，
S_△ADF=$\frac{1}{2}$×1×2=1，
S_△ABF=$\frac{1}{2}$×1×$\sqrt{{1}^{2}{+2}^{2}}$=$\frac{\sqrt{5}}{2}$，
S_△BCE=$\frac{1}{2}$×1×1=$\frac{1}{2}$，
△BEF中，BE=$\sqrt{2}$，BF=$\sqrt{{2}^{2}{+（\sqrt{2}）}^{2}}$=$\sqrt{6}$，EF=$\sqrt{2}$，
∴S_△BEF=$\frac{1}{2}$×$\sqrt{6}$×$\sqrt{{（\sqrt{2}）}^{2}{-（\frac{\sqrt{6}}{2}）}^{2}}$=$\frac{\sqrt{3}}{2}$；
∴空间几何体ABCDFE的表面积为
S=S_{正方形ABCD}+S_{直角梯形DCEF}+S_△ADF+S_△ABF+S_△BCE+S_△BEF
=1+$\frac{3}{2}$+1+$\frac{\sqrt{5}}{2}$+$\frac{1}{2}$+$\frac{\sqrt{3}}{2}$=4+$\frac{\sqrt{5}+\sqrt{3}}{2}$．

点评 本题考查了折叠问题，解题时要分析折叠前、后的位置关系、几何量的变与不变，应画好图形，正确识图；另外解决空间问题的基本思路是利用转化思想，一是空间问题转化为平面几何问题，二是平行、垂直关系中线线、线面与面面关系的互相转化，是综合性题目．