
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 由题意得到所有的S值判断①,利用作差法求得S的最小值结合向量垂直、平行及数量积运算判断②③④,则答案可求.
解答 解:由题意可知,S=$\overrightarrow{{x}_{1}}$•$\overrightarrow{{y}_{1}}$+$\overrightarrow{{x}_{2}}$•$\overrightarrow{{y}_{2}}$+$\overrightarrow{{x}_{3}}$•$\overrightarrow{{y}_{3}}$+$\overrightarrow{{x}_{4}}$•$\overrightarrow{{y}_{4}}$ 有三个值,分别为$2{\overrightarrow{a}}^{2}+2{\overrightarrow{b}}^{2}$、${\overrightarrow{a}}^{2}+{\overrightarrow{b}}^{2}+2\overrightarrow{a}•\overrightarrow{b}$、$4\overrightarrow{a}•\overrightarrow{b}$.
∴①正确;
∵$2{\overrightarrow{a}}^{2}+2{\overrightarrow{b}}^{2}$-$4\overrightarrow{a}•\overrightarrow{b}$=$2(\overrightarrow{a}-\overrightarrow{b})^{2}≥0$,
${\overrightarrow{a}}^{2}+{\overrightarrow{b}}^{2}+2\overrightarrow{a}•\overrightarrow{b}$-$4\overrightarrow{a}•\overrightarrow{b}$=$(\overrightarrow{a}-\overrightarrow{b})^{2}≥0$,
∴${S}_{min}=4\overrightarrow{a}•\overrightarrow{b}$.
若$\overrightarrow{a}$⊥$\overrightarrow{b}$,则Smin=0与|$\overrightarrow{b}$|无关,∴②正确;
若$\overrightarrow{a}$∥$\overrightarrow{b}$,则Smin=$4|\overrightarrow{a}||\overrightarrow{b}|cos<\overrightarrow{a},\overrightarrow{b}>$,与|$\overrightarrow{b}$|有关,∴③错误;
若|$\overrightarrow{b}$|=2|$\overrightarrow{a}$,Smin=4${|\overrightarrow{a}|}^{2}$,则cos<$\overrightarrow{a},\overrightarrow{b}$>=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}||\overrightarrow{b}|}=\frac{|\overrightarrow{a}{|}^{2}}{2|\overrightarrow{a}{|}^{2}}=\frac{1}{2}$,$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为$\frac{π}{3}$,故④正确.
∴命题中正确的个数为3个.
故选:D.
点评 本题考查命题的真假判断与应用,考查平面向量的数量积运算,考查逻辑思维能力与推理运算能力,是中档题.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:填空题
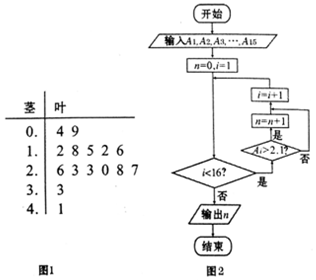 图1是随机抽取的15户居民月均用水量(单位:t)的茎叶图,月均用水量依次记为A1、A2、…A15,图2是统计茎叶图中月均用水量在一定范围内的频数的一个程序框图,那么输出的结果n=7.
图1是随机抽取的15户居民月均用水量(单位:t)的茎叶图,月均用水量依次记为A1、A2、…A15,图2是统计茎叶图中月均用水量在一定范围内的频数的一个程序框图,那么输出的结果n=7.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -15 | B. | 1 | C. | 5 | D. | 21 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $2+\sqrt{5}$ | B. | $2+2\sqrt{5}$ | C. | $4+\sqrt{5}$ | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
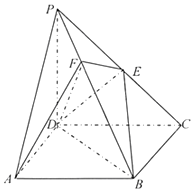 《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.
《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {4} | B. | {1,2,4,6,7} | C. | {3,5} | D. | {1,7} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com