
某中学举行了一次“环保知识竞赛”活动.为了了解本次竞赛学生成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100分)作为样本(样本容量为n)进行统计.按照 ,
,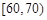 ,
, ,
,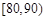 ,
,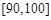 的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在
的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在 ,
,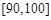 的数据).
的数据).
频率分布直方图 茎叶图
(1)求样本容量n和频率分布直方图中x、y的值;
(2)在选取的样本中,从竞赛成绩是80分以上(含80分)的同学中随机抽取2名同学到市政广场参加环保知识宣传的志愿者活动,求所抽取的2名同学来自不同组的概率.
(1)0.004,0.030;(2)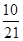 .
.
解析试题分析:(1)由频率分布直方图可求出分数在50到60的频率,由茎叶图可得出分数在50到60的人数,
由此可得样本容量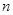 .又由茎叶图可得分数在90到100的人数,从而求得
.又由茎叶图可得分数在90到100的人数,从而求得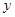 .这样除了60到70分这一组之外,其余各组的频率都知道了,也就可以求出
.这样除了60到70分这一组之外,其余各组的频率都知道了,也就可以求出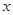 的值了.(2)由(1)可知,分数在[80,90)有5人,分数在[90,100)有2人,共7人.将这7人用不同字母表示出来,然后将取出2人所有基本事件(即可能出现的结果)一一列出,数出来自不同组的基本事件事件的个数,由古典概型的概率公式即得所求概率.
的值了.(2)由(1)可知,分数在[80,90)有5人,分数在[90,100)有2人,共7人.将这7人用不同字母表示出来,然后将取出2人所有基本事件(即可能出现的结果)一一列出,数出来自不同组的基本事件事件的个数,由古典概型的概率公式即得所求概率.
(1)由题意可知,样本容量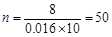
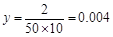
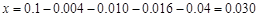 .
.
(2)由题意可知,分数在[80,90)有5人,分别记为a,b,c,d,e,分数在[90,100)有2人,分别记为F,G.从竞赛成绩是80分以上(含80分)的同学中随机抽取2名同学有如下种情形:(a,b),(a,c),(a,d),(a,e),(a,F),(a,G),(b,c),(b,d),(b,e),(b,F),(b,G),(c,d),(c,e),(c,F),(c,G),(d,e),(d,F),(d,G),(e,F),(e,G),(F,G),共有21个基本事件;其中符合“抽取的2名同学来自不同组”的基本事件有(a,F),(a,G),(b,F),(b,G),(c,F),(c,G),(d,F),(d,G),(e,F),(e,G),共10个,所以抽取的2名同学来自不同组的概率 .
.
考点:1、用样本估计总体,2、古典概率.


科目:高中数学 来源: 题型:解答题
春节前,有超过20万名广西,四川等省籍的外来务工人员选择驾乘摩托车沿321国道长途跋涉返乡过年,为防止摩托车驾驶人员因长途疲劳驾驶,手脚僵硬影响驾驶操作而引发交通事故,肇庆市公安交警部门在321国道沿线设立了多个长途行驶摩托车驾驶人员休息站,让过往返乡过年的摩托车驾驶人员有一个停车休息的场所.交警小李在某休息站连续5天对进站休息的驾驶人员每隔50辆摩托车就进行省籍询问一次,询问结果如图所示.
(1)问交警小李对进站休息的驾驶人员的省籍询问采用的是什么抽样方法;
(2)用分层抽样的方法对被询问了省籍的驾驶人员进行抽样,若广西籍的被抽取了5名,则四川籍的应抽取几名?
(3)在上述抽出的驾驶人员中任取2名,求至少有1名驾驶人员是广西籍的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某普通高中共有教师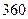 人,分为三个批次参加研修培训,在三个批次中男、女教师人数如下表所示:
人,分为三个批次参加研修培训,在三个批次中男、女教师人数如下表所示:
| | 第一批次 | 第二批次 | 第三批次 |
| 女教师 | 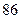 |  |  |
| 男教师 | 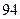 | 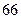 |  |
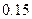 、
、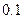 .
.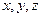 的值;
的值;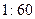 的比例抽取教师进行问卷调查,三个批次被选取的人数分别是多少?
的比例抽取教师进行问卷调查,三个批次被选取的人数分别是多少?查看答案和解析>>
科目:高中数学 来源: 题型:解答题
由某种设备的使用年限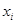 (年)与所支出的维修费
(年)与所支出的维修费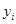 (万元)的数据资料算得如下结果,
(万元)的数据资料算得如下结果,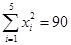 ,
,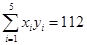 ,
,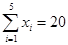 ,
,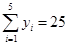 .
.
(1)求所支出的维修费y对使用年限x的线性回归方程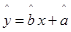 ;
;
(2)①判断变量x与y之间是正相关还是负相关;
②当使用年限为8年时,试估计支出的维修费是多少.
(附:在线性回归方程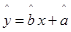 中,)
中,)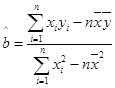 ,
,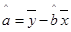 ,其中
,其中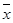 ,
, 为样本平均值.)
为样本平均值.)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某种产品的广告费支出x与销售额 (单位:百万元)之间有如下对应数据:
(单位:百万元)之间有如下对应数据:
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 50 | 60 | 70 |
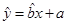 .
. ,你可得到什么结论?
,你可得到什么结论?查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某校100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60][60,70][70,80][80,90][90,100].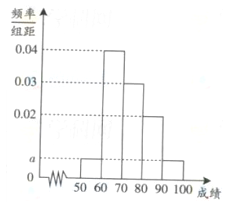
(1)求图中a的值;
(2)根据频率分布直方图,估计这100名学生语文成绩的平均分;
(3)若这100名学生语文成绩某些分数段的人数(x)与数学成绩相应分数段的人数(y)之比如下表所示,求数学成绩在[50,90)之外的人数.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为预防X病毒爆发,某生物技术公司研制出一种X病毒疫苗,为测试该疫苗的有效性(若疫苗有效的概率小于90%,则认为测试没有通过),公司选定2000个样本分成三组,测试结果如下表:
| 分组 |  组 组 | 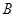 组 组 |  组 组 |
| 疫苗有效 | 673 | 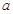 | 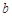 |
| 疫苗无效 | 77 | 90 | 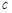 |
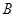 组疫苗有效的概率是0.33.
组疫苗有效的概率是0.33. 组抽取样本多少个?
组抽取样本多少个?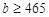 ,
,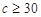 ,求通过测试的概率.
,求通过测试的概率.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某学校为了选拔学生参加“XX市中学生知识竞赛”,先在本校进行选拔测试(满分150分),若该校有100名学生参加选拔测试,并根据选拔测试成绩作出如图所示的频率分布直方图.
(1)根据频率分布直方图,估算这100名学生参加选拔测试的平均成绩;
(2)该校推荐选拔测试成绩在110以上的学生代表学校参加市知识竞赛,为了了解情况,在该校推荐参加市知识竞赛的学生中随机抽取2人,求选取的两人的选拔成绩在频率分布直方图中处于不同组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某地区有小学21所,中学14所,大学7所,现采用分层抽样的方法从这些学校中抽取6所学校对学生进行视力调查.
(1)求应从小学、中学、大学中分别抽取的学校数目;
(2)若从抽取的6所学校中随机抽取2所学校做进一步数据分析,
①列出所有可能的抽取结果;
②求抽取的2所学校均为小学的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com