
某校100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60][60,70][70,80][80,90][90,100].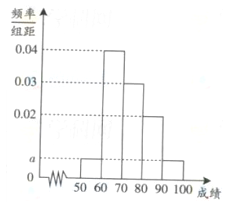
(1)求图中a的值;
(2)根据频率分布直方图,估计这100名学生语文成绩的平均分;
(3)若这100名学生语文成绩某些分数段的人数(x)与数学成绩相应分数段的人数(y)之比如下表所示,求数学成绩在[50,90)之外的人数.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
某电视台在一次对文艺节目和新闻节目观众的抽样调查中,随机抽取了100名电视观众,相关数据如下表所示:
| | 文艺节目 | 新闻节目 | 总计 |
| 20岁到40岁 | 40 | 20 | 60 |
| 40岁以上 | 15 | 25 | 40 |
| 总计 | 55 | 45 | 100 |
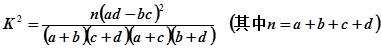
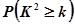 | 0.05 | 0.01 | 0.005 | 0.001 |
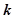 | 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某种产品的广告费支出z与销售额y(单位:万元)之间有如下对应数据:
若广告费支出z与销售额y回归直线方程为多一6.5z+n(n∈R).
(1)试预测当广告费支出为12万元时,销售额是多少?
(2)在已有的五组数据中任意抽取两组,求至少有一组数据其预测值与实际值之差的绝对值不超过5的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某学校高一年学生在某次数学单元测试中,成绩在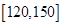 的频数分布表如下:
的频数分布表如下:
| 分数 |  | 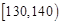 | 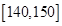 |
| 频数 | 60 | 20 | 20 |
 ,
,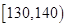 和
和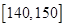 的同学中共抽取
的同学中共抽取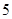 人,其中成绩在
人,其中成绩在 的有几人?
的有几人?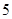 人中,任取
人中,任取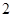 人,求成绩在
人,求成绩在 和
和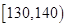 中各有
中各有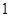 人的概率?
人的概率?查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某中学举行了一次“环保知识竞赛”活动.为了了解本次竞赛学生成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100分)作为样本(样本容量为n)进行统计.按照 ,
,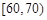 ,
, ,
,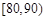 ,
,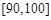 的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在
的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在 ,
,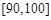 的数据).
的数据).
频率分布直方图 茎叶图
(1)求样本容量n和频率分布直方图中x、y的值;
(2)在选取的样本中,从竞赛成绩是80分以上(含80分)的同学中随机抽取2名同学到市政广场参加环保知识宣传的志愿者活动,求所抽取的2名同学来自不同组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某食品厂为了检查一条自动包装流水线的生产情况,从该流水线上随机抽取40件产品作为样本,测得它们的重量(单位:克),将重量按如下区间分组: ,
, ,
,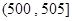 ,
, ,
,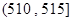 ,得到样本的频率分布直方图(如图所示).若规定重量超过495克但不超过510克的产品为合格产品,且视频率为概率,回答下列问题:
,得到样本的频率分布直方图(如图所示).若规定重量超过495克但不超过510克的产品为合格产品,且视频率为概率,回答下列问题:
(1)在上述抽取的40件产品中任取2件,设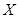 为合格产品的数量,求
为合格产品的数量,求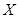 的分布列和数学期
的分布列和数学期
望 ;
;
(2)若从流水线上任取3件产品,求恰有2件合格产品的概率.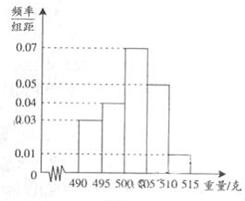
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
以下茎叶图记录了甲,乙两组各三名同学在期末考试中的数学成绩(满分为100分).乙组记录中有一个数字模糊,无法确认,假设这个数字具有随机性,并在图中以a表示.
(1)若甲,乙两个小组的数学平均成绩相同,求a的值.
(2)求乙组平均成绩超过甲组平均成绩的概率.
(3)当a=2时,分别从甲,乙两组同学中各随机选取一名同学,求这两名同学的数学成绩之差的绝对值为2分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某工厂有工人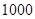 人,其中
人,其中 名工人参加过短期培训(称为
名工人参加过短期培训(称为 类工人),另外
类工人),另外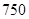 名工人参加过长期培训(称为
名工人参加过长期培训(称为 类工人).现用分层抽样的方法(按
类工人).现用分层抽样的方法(按 类、
类、 类分二层)从该工厂的工人中共抽查
类分二层)从该工厂的工人中共抽查 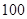 名工人,调查他们的生产能力(此处的生产能力指一天加工的零件数).
名工人,调查他们的生产能力(此处的生产能力指一天加工的零件数).
(1) 类工人和
类工人和 类工人中各抽查多少工人?
类工人中各抽查多少工人?
(2)从 类工人中的抽查结果和从
类工人中的抽查结果和从 类工人中的抽查结果分别如下表1和表2.
类工人中的抽查结果分别如下表1和表2.
表1
| 生产能力分组 | 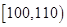 | 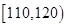 |  | 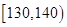 | 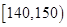 |
| 人数 | 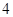 |  |  | 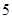 |  |
| 生产能力分组 | 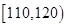 |  | 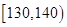 | 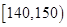 |
| 人数 |  |  |  |  |
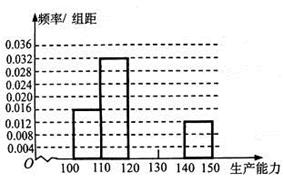
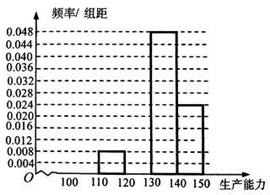
 、
、 ,再完成下列频率分布直方图;
,再完成下列频率分布直方图; 类工人和
类工人和 类工人生产能力的平均数,并估计该工厂工人的生产能力的平均数(同一组
类工人生产能力的平均数,并估计该工厂工人的生产能力的平均数(同一组查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某电视台组织部分记者,用“10分制”随机调查某社区居民的幸福指数.现从调查人群中随机抽取16名,如图所示的茎叶图记录了他们的幸福指数的得分(以小数点前的一位数字为茎,小数点后的一位数字为叶):
(1)指出这组数据的众数和中位数;
(2)若幸福指数不低于9.5分,则称该人的幸福指数为“极幸福”.求从这16人中随机选取3人,至多有1人是“极幸福”的概率;
(3)以这16人的样本数据来估计整个社区的总体数据,若从该社区(人数很多)任选3人,记 表示抽到“极幸福”的人数,求
表示抽到“极幸福”的人数,求 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com