
函数f(x)=x3-bx2+1有且仅有两个不同零点,则b的值为( )
A.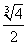 B.
B.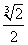
C.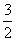
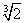 D.不确定
D.不确定
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:
某农场,可以全部种植水果、蔬菜、稻米、甘蔗等农作物,且产品全部供应距农场d(km)(d<200km)的中心城市,其产销资料如表:当距离d达到n(km)以上时,四种农作物中以全部种植稻米的经济效益最高.(经济效益=市场销售价值-生产成本-运输成本),则n的值为________.
| 作物 项目 | 水果 | 蔬菜 | 稻米 | 甘蔗 |
| 市场价格(元/kg) | 8 | 3 | 2 | 1 |
| 生产成本(元/kg) | 3 | 2 | 1 | 0.4 |
| 运输成本(元/kg·km) | 0.06 | 0.02 | 0.01 | 0.01 |
| 单位面积相对产量(kg) | 10 | 15 | 40 | 30 |
查看答案和解析>>
科目:高中数学 来源: 题型:
设f(x)是定义在R上的偶函数,对任意x∈R,都有f(x)=f(x+4),且当x∈[-2,0]时,f(x)=(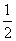 )x-1,若在区间(-2,6]内关于x的方程f(x)-loga(x+2)=0(a>1)恰有三个不同的实数根,则a的取值范围为________.
)x-1,若在区间(-2,6]内关于x的方程f(x)-loga(x+2)=0(a>1)恰有三个不同的实数根,则a的取值范围为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
某流程图如图所示,现输入如下四个函数,则可以输出的函数是( )
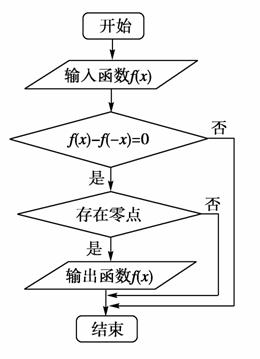
A.f(x)=tanx B.f(x)=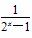 +
+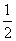
C.f(x)=x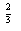 D.f(x)=lgsinx
D.f(x)=lgsinx
查看答案和解析>>
科目:高中数学 来源: 题型:
在直角坐标系xOy中,点M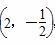 ,点F为抛物线C:y=mx2(m>0)的焦点,线段MF恰被抛物线C平分.
,点F为抛物线C:y=mx2(m>0)的焦点,线段MF恰被抛物线C平分.
(1)求m的值;
(2)过点M作直线l交抛物线C于A,B两点,设直线FA,FM,FB的斜率分别为k1,k2,k3,问k1,k2,k3能否成公差不为零的等差数列?若能,求直线l的方程;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com