解:(I)如图,作PO⊥AC,垂足为O,连接OB
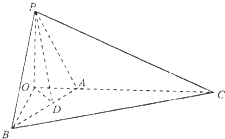
由已知得△POC≌△BOC,可得BO⊥AC.
∵AP=AB=AC=2,∠BAC=∠PAC=120°.
∴PO=0B=PAsin60°=

∵平面PAC⊥平面BAC,平面PAC∩平面BAC=AC,PO⊥AC
∴PO⊥平面BAC,结合OB?平面BAC,可得PO⊥OB
由此可得PB=

PO=

(II)如图,作OD⊥AB于D,连接OD,
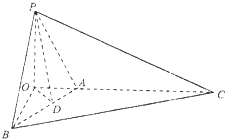
∵PO⊥平面BAC,可得OD是PD在平面ABC内的射影
∴PD⊥AB,得∠PDO就是二面角P-AB-O的平面角,等于二面角P-AB-C的补角
∵Rt△BOD中,OD=BOsin∠OBD=POsin30°=

PO
∴tan∠PDO=
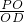
=2,可得∠PDO=arctan2
由此可得二面角P-AB-O的平面角等于arctan2,
即得二面角P-AB-C的大小为π-arctan2.
分析:(I)作PO⊥AC,垂足为O,连接OB.根据△POC≌△BOC得到对应高线相等,即PO=0B=PAsin60°=

.由面面垂直的性质定理,证出PO⊥平面BAC,可得PO⊥OB,从而得到PB=

PO=

;
(II)如图,作OD⊥AB于D,连接OD,根据PO⊥平面BAC结合三垂直线定理,得到∠PDO就是二面角P-AB-O的平面角,等于二面角P-AB-C的补角.Rt△BOD中利用解三角形的知识,结合题中数据算出tan∠PDO,从而得到二面角P-AB-C的大小.
点评:本题给出顶角为120°的两个等腰三角形有公共的腰且所在的平面相互垂直,求线段PB之长并求二面角的大小,着重考查了面面垂直、线面垂直的判定与性质、利用三垂线定理作二面的平面角和解直角三角形等知识,属于中档题.

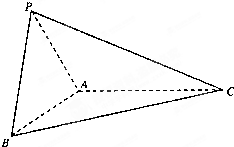 如图,三棱锥P-ABC中,平面PAC⊥平面BAC,AP=AB=AC=2,∠BAC=∠PAC=120°.
如图,三棱锥P-ABC中,平面PAC⊥平面BAC,AP=AB=AC=2,∠BAC=∠PAC=120°.

 PO=
PO=

 PO
PO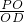 =2,可得∠PDO=arctan2
=2,可得∠PDO=arctan2 .由面面垂直的性质定理,证出PO⊥平面BAC,可得PO⊥OB,从而得到PB=
.由面面垂直的性质定理,证出PO⊥平面BAC,可得PO⊥OB,从而得到PB= PO=
PO= ;
;

 如图,三棱锥P-ABC中,PC⊥平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD⊥平面PAB
如图,三棱锥P-ABC中,PC⊥平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD⊥平面PAB (2006•石景山区一模)如图,三棱锥P-ABC中,
(2006•石景山区一模)如图,三棱锥P-ABC中, (2012•湖南模拟)如图,三棱锥P-ABC中,侧面PAC⊥底面ABC,∠APC=90°,且AB=4,AP=PC=2,BC=2
(2012•湖南模拟)如图,三棱锥P-ABC中,侧面PAC⊥底面ABC,∠APC=90°,且AB=4,AP=PC=2,BC=2 (2012•德阳二模)如图,三棱锥P-ABC中,PA丄面ABC,∠ABC=90°,PA=AB=1,BC=2,则P-ABC的外接球的表面积为
(2012•德阳二模)如图,三棱锥P-ABC中,PA丄面ABC,∠ABC=90°,PA=AB=1,BC=2,则P-ABC的外接球的表面积为 如图在三棱锥P-ABC中,AB⊥PC,AC=2,BC=4,AB=2
如图在三棱锥P-ABC中,AB⊥PC,AC=2,BC=4,AB=2