
分析 利用△PF1F2的面积为1,PF1⊥PF2,可得|PF1|•|PF2|=2,利用勾股定理,结合双曲线的定义,即可求双曲线的方程.
解答 解:由题意,c=$\sqrt{5}$,
因为△PF1F2的面积为1,PF1⊥PF2,
所以|PF1|•|PF2|=2,
又|PF1|2+|PF2|2=|F1F2|2=4c2=20,
从而(|PF1|-|PF2|)2=|PF1|2+|PF2|2-2|PF1|•|PF2|=20-4=16,即4a2=16,a=2,
所以b2=c2-a2=5-4=1,
所以双曲线的方程为$\frac{{x}^{2}}{4}$-y2=1,
故答案为:$\frac{{x}^{2}}{4}$-y2=1.
点评 本题考查双曲线的标准方程,考查勾股定理,考查学生的计算能力,属于中档题.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:高中数学 来源: 题型:解答题
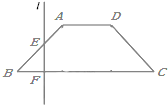 如图,已知底角为45°的等腰梯形ABCD,底边BC长为7cm,腰长为2$\sqrt{2}$cm,当一条垂直于底边BC(垂足为F)的直线l从左至右移动(与梯形ABCD有公共点)时,直线l把梯形分成两部分,令BF=x,
如图,已知底角为45°的等腰梯形ABCD,底边BC长为7cm,腰长为2$\sqrt{2}$cm,当一条垂直于底边BC(垂足为F)的直线l从左至右移动(与梯形ABCD有公共点)时,直线l把梯形分成两部分,令BF=x,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{1}{2}$,-$\frac{\sqrt{3}}{4}$) | B. | (-$\frac{1}{2}$,-$\frac{\sqrt{3}}{4}$] | C. | [0,-$\frac{\sqrt{3}}{4}$] | D. | (-$\frac{2}{3}$,-$\frac{1}{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{4}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 11 | B. | 99 | C. | 120 | D. | 121 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com