
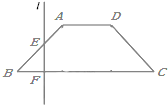
 如图,已知底角为45°的等腰梯形ABCD,底边BC长为7cm,腰长为2$\sqrt{2}$cm,当一条垂直于底边BC(垂足为F)的直线l从左至右移动(与梯形ABCD有公共点)时,直线l把梯形分成两部分,令BF=x,
如图,已知底角为45°的等腰梯形ABCD,底边BC长为7cm,腰长为2$\sqrt{2}$cm,当一条垂直于底边BC(垂足为F)的直线l从左至右移动(与梯形ABCD有公共点)时,直线l把梯形分成两部分,令BF=x,分析 (1)可以通过分类讨论明确图形的特征,再根据图形形状求出函数的解析式;
(2)利用函数的解析式求出集合A,再根据A∪B=B得到A⊆B,得$\left\{\begin{array}{l}{a+2≥3}\\{a-2≤0}\end{array}\right.$,解得即可.
解答 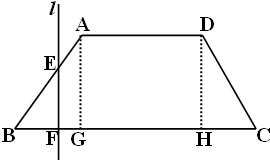 解:过点A.D分别作AG⊥BC,DH⊥BC,垂足分别是G,H.
解:过点A.D分别作AG⊥BC,DH⊥BC,垂足分别是G,H.
∵ABCD是等腰梯形,底角为45°,AB=2$\sqrt{2}$cm,
∴BG=AG=DH=HC=2cm,
又∵BC=7cm,
∴AD=GH=3cm,
①当点F在BG上时,
即x∈(0,2]时,f(x)=$\frac{1}{2}$x2;
②当点F在GH上时,
即x∈(2,5]时,f(x)=2+(x-2)-2=2x-2.
③当点F在HC上时,
即x∈(5,7)时,y=S五边形ABFED=S梯形ACD-S三角形CEF
f(x)=-$\frac{1}{2}$(x-7)2+10,
∴函数解析式为f(x)=$\left\{\begin{array}{l}{\frac{1}{2}{x}^{2},0<x≤2}\\{2x-2,2<x≤5}\\{-\frac{1}{2}(x-7)^{2}+10,5<x≤7}\end{array}\right.$
(2)A={x|f(x)<4},
当0<x≤2时,f(x)=$\frac{1}{2}$x2<4,解得0<x≤2,
当x∈(2,5]时,f(x)=2x-2<4,解得2<x<3,
当x∈(5,7)时,f(x)=-$\frac{1}{2}$(x-7)2+10<4,此时解集为空集,
综上所述A=(0,3),
B={x|a-2<x<a+2},A∪B=B
∴A⊆B,得$\left\{\begin{array}{l}{a+2≥3}\\{a-2≤0}\end{array}\right.$,解得1≤a≤2,
∴a的取值范围为[1,2].
点评 本题考查了函数的解析式、以及函数的值域,和集合和集合的关系,属于中档题.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| x | -1 | 0 | 1 | 2 | 3 |
| ex | 0.37 | 1 | 2.72 | 7.39 | 20.09 |
| x+6 | 5 | 6 | 7 | 8 | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{3}{4}$ | B. | $\frac{3}{5}$ | C. | -$\frac{4}{5}$ | D. | -$\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{1}{5}$ | C. | $\frac{3}{10}$ | D. | $\frac{2}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com