
| x | -1 | 0 | 1 | 2 | 3 |
| ex | 0.37 | 1 | 2.72 | 7.39 | 20.09 |
| x+6 | 5 | 6 | 7 | 8 | 9 |
分析 求出过点(1,2)且在坐标轴上的截距相等的直线方程,可判断①;
求解不等式f(x)>2x+4,可判断②;
分析方程ex-x-6=0根的位置,可判断③;
求出椭圆的离心率,可判断④;
求出实数a的范围,可判断⑤;
求出函数的零点个数,可判断⑥.
解答 解:①过点(1,2)且在坐标轴上的截距相等的直线方程是x+y=3或2x-y=0,故错误;
②函数f(x)的定义域是R,f(-1)=2,对?x∈R,f′(x)>2,
g(x)=f(x)-2x满足g′(x)=f′(x)-2>0,
即g(x)=f(x)-2x为增函数,且g(-1)=4
则f(x)>2x+4可化为:g(x)>4=g(-1)
解得:x∈(-1,+∞),故正确;
③根据表格中的数据,可以判定方程ex-x-6=0的一个根所在的区间为(2,3),正确;
④已知双曲线的渐近线方程是5x±12y=0,
当焦点在x轴上时,则以双曲线的顶点为焦点,以双曲线的焦点为顶点的椭圆的离心率e=$\frac{12}{13}$;
当焦点在y轴上时,则以双曲线的顶点为焦点,以双曲线的焦点为顶点的椭圆的离心率e=$\frac{5}{13}$;
综上可得:以双曲线的顶点为焦点,以双曲线的焦点为顶点的椭圆的离心率e=$\frac{12}{13}$,错误;
⑤解:f′(x)=$\frac{2}{x}$+2,
∴f(x)在(0,+∞)上单调递增;
∴由f[f(b)]=b,得f(b)=b;
则f(x)=x在[1,e]上有根;
即2lnx+2x-a=x;
∴a=2lnx+x;
令h(x)=2lnx+x,h′(x)=$\frac{2}{x}$+1>0;
∴h(x)在[1,e]上单调递增;
∴h(x)min=h(1)=1,h(x)max=h(e)=2+e;
∴a∈[1,2+e];
即实数a的取值范围是[1,2+e].正确;
⑥由题意得,f(x)=(1+x-$\frac{{x}^{2}}{2}$+$\frac{{x}^{3}}{3}$-$\frac{{x}^{4}}{4}$+…-$\frac{{x}^{2014}}{2014}$+$\frac{{x}^{2015}}{2015}$)cos2x=0,
①当cos2x=0时,由x∈[-3,3]得2x∈[-6,6],
解得x=$±\frac{π}{4}$或±$\frac{3π}{4}$;
②当1+x-$\frac{{x}^{2}}{2}$+$\frac{{x}^{3}}{3}$-$\frac{{x}^{4}}{4}$+…-$\frac{{x}^{2014}}{2014}$+$\frac{{x}^{2015}}{2015}$=0时,
设g(x)=1+x-$\frac{{x}^{2}}{2}$+$\frac{{x}^{3}}{3}$-$\frac{{x}^{4}}{4}$+…-$\frac{{x}^{2014}}{2014}$+$\frac{{x}^{2015}}{2015}$,
则g′(x)=1-x+x2-x3+…-x2013+x2014=$\left\{\begin{array}{l}2015,x=-1\\ \frac{1+{x}^{2015}}{1+x},x≠-1\end{array}\right.$,
∴g′(x)>0,则g(x)在[-3,3]上单调递增,
∵g(-3)<0,g(3)>0,
∴g(x)在[-3,3]上有且仅有1个零点,
显然g($±\frac{π}{4}$)≠0、g(±$\frac{3π}{4}$)≠0,
所以f(x)共有5个零点,正确;
故答案为:②③⑤⑥
点评 本题以命题的真假判断与应用为载体,考查直线方程,零点个数,抽象不等式的解法等知识点,难度中档.


 口算能手系列答案
口算能手系列答案科目:高中数学 来源: 题型:解答题
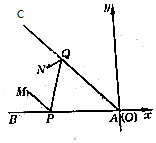 如图,∠BAC为伸入江中的半岛,AB和AC为两江岸,M处为水文站,N处为电讯局,现欲在两江岸AB和AC上各建一个水文观测点P、Q,现测得∠BAC=45°,当直角坐标系以点A为坐标原点且以直线BA为x轴时,测得M(-4,1)、N(-3,2).P、Q两点应建在何处才能使路程MPQN最短?
如图,∠BAC为伸入江中的半岛,AB和AC为两江岸,M处为水文站,N处为电讯局,现欲在两江岸AB和AC上各建一个水文观测点P、Q,现测得∠BAC=45°,当直角坐标系以点A为坐标原点且以直线BA为x轴时,测得M(-4,1)、N(-3,2).P、Q两点应建在何处才能使路程MPQN最短?查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①③④ | B. | ②④⑤ | C. | ③④⑤ | D. | ②③⑤ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
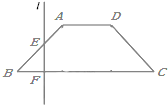 如图,已知底角为45°的等腰梯形ABCD,底边BC长为7cm,腰长为2$\sqrt{2}$cm,当一条垂直于底边BC(垂足为F)的直线l从左至右移动(与梯形ABCD有公共点)时,直线l把梯形分成两部分,令BF=x,
如图,已知底角为45°的等腰梯形ABCD,底边BC长为7cm,腰长为2$\sqrt{2}$cm,当一条垂直于底边BC(垂足为F)的直线l从左至右移动(与梯形ABCD有公共点)时,直线l把梯形分成两部分,令BF=x,查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com