
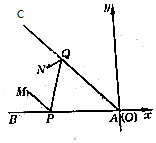
 如图,∠BAC为伸入江中的半岛,AB和AC为两江岸,M处为水文站,N处为电讯局,现欲在两江岸AB和AC上各建一个水文观测点P、Q,现测得∠BAC=45°,当直角坐标系以点A为坐标原点且以直线BA为x轴时,测得M(-4,1)、N(-3,2).P、Q两点应建在何处才能使路程MPQN最短?
如图,∠BAC为伸入江中的半岛,AB和AC为两江岸,M处为水文站,N处为电讯局,现欲在两江岸AB和AC上各建一个水文观测点P、Q,现测得∠BAC=45°,当直角坐标系以点A为坐标原点且以直线BA为x轴时,测得M(-4,1)、N(-3,2).P、Q两点应建在何处才能使路程MPQN最短? 分析 分别求出M关于AB对称的点M1为(-4,-1),N关于AC对称的点N1为(-2,3),所以M1,N1与AB,AC 的交点就是P,Q点时,MPQN最短就是M1N1的距离,即可得出结论.
解答 解:分别求出M关于AB对称的点M1为(-4,-1),N关于AC对称的点N1为(-2,3),
所以M1,N1与AB,AC 的交点就是P,Q点时,MPQN最短就是M1N1的距离,
M1N1的直线方程为y=2x+7交AB点为P(-$\frac{7}{2}$,0),
交AC点为Q,AC方程式为y=-x所以Q(-$\frac{7}{3}$,$\frac{7}{3}$).
点评 本题考查利用数学知识解决实际问题,考查学生的计算能力,属于中档题.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$+$\frac{1}{2}$i | B. | $\frac{1}{2}$+$\frac{1}{2}$i | C. | $\frac{1}{2}$-$\frac{1}{2}$i | D. | -$\frac{1}{2}$-$\frac{1}{2}$i |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| x | -1 | 0 | 1 | 2 | 3 |
| ex | 0.37 | 1 | 2.72 | 7.39 | 20.09 |
| x+6 | 5 | 6 | 7 | 8 | 9 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com