
分析 (Ⅰ)由f($\frac{1}{2}$)=$\frac{2}{5}$.可求a的值,再由奇偶性的定义,可判断函数f(x)的奇偶性;
(Ⅱ)证法一:设-1<x1<x2<1,作差判断f(x1)的f(x2)大小,根据单调性的定义,可得:函数f(x)在(-1,1)上是增函数f(x1)<f(x2),
证法二:求导,由当x∈(-1,1)时,f′(x)>0恒成立,可得:函数f(x)在(-1,1)上是增函数
解答 解(Ⅰ)∵函数f(x)=$\frac{ax}{{1+{x^2}}}$满足f($\frac{1}{2}$)=$\frac{2}{5}$.
∴$\frac{\frac{1}{2}a}{\frac{5}{4}}$=$\frac{2}{5}$.
解得:a=1,
∴函数f(x)=$\frac{x}{1+{x}^{2}}$的定义域R关于原点对称,
又由$f(-x)=\frac{-x}{{{x^2}+1}}=-f(x)$,
∴f(x)为奇函数…(3分)
(Ⅱ)证法一:设-1<x1<x2<1,
则x1-x2<0,1-x1x2>0,
∴$f({x_1})-f({x_2})=\frac{{({x_1}-{x_2})(1-{x_1}{x_2})}}{(1+x_1^2)(1+x_2^2)}$<0,
即f(x1)<f(x2),
∴函数f(x)在(-1,1)上是增函数…(8分)
证法二:∵f(x)=$\frac{x}{1+{x}^{2}}$,
∴f′(x)=$\frac{1-{x}^{2}}{(1+{x}^{2})^{2}}$,
当x∈(-1,1)时,
f′(x)>0恒成立,
∴函数f(x)在(-1,1)上是增函数…(8分)
点评 本题考查的知识点是函数的单调性,函数的奇偶性,难度中档.


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:高中数学 来源: 题型:选择题
| A. | (1.4,2) | B. | (1,1.4) | C. | (1,1.5) | D. | (1.5,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左右焦点分别为F1,F2,抛物线y2=4x与椭圆C有相同的焦点,点P为抛物线与椭圆C在第一象限的交点,且|PF1|=$\frac{7}{3}$.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左右焦点分别为F1,F2,抛物线y2=4x与椭圆C有相同的焦点,点P为抛物线与椭圆C在第一象限的交点,且|PF1|=$\frac{7}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
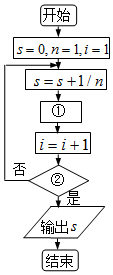 如图给出的是计算1+$\frac{1}{3}$+$\frac{1}{5}$+…+$\frac{1}{2017}$的值的一个程序框图,则图中执行框中的①处和判断框中的②处应填的语句是( )
如图给出的是计算1+$\frac{1}{3}$+$\frac{1}{5}$+…+$\frac{1}{2017}$的值的一个程序框图,则图中执行框中的①处和判断框中的②处应填的语句是( )| A. | n=n+1,i>1009 | B. | n=n+2,i>1009 | C. | n=n+1,i>1010 | D. | n=n+2,i>1010 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
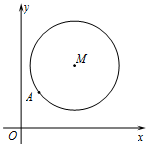 如图,在平面直角坐标系xOy中,已知以M为圆心的圆M:x2+y2-12x-14y+60=0及其上一点A(2,4).
如图,在平面直角坐标系xOy中,已知以M为圆心的圆M:x2+y2-12x-14y+60=0及其上一点A(2,4).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
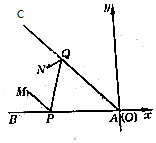 如图,∠BAC为伸入江中的半岛,AB和AC为两江岸,M处为水文站,N处为电讯局,现欲在两江岸AB和AC上各建一个水文观测点P、Q,现测得∠BAC=45°,当直角坐标系以点A为坐标原点且以直线BA为x轴时,测得M(-4,1)、N(-3,2).P、Q两点应建在何处才能使路程MPQN最短?
如图,∠BAC为伸入江中的半岛,AB和AC为两江岸,M处为水文站,N处为电讯局,现欲在两江岸AB和AC上各建一个水文观测点P、Q,现测得∠BAC=45°,当直角坐标系以点A为坐标原点且以直线BA为x轴时,测得M(-4,1)、N(-3,2).P、Q两点应建在何处才能使路程MPQN最短?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com