
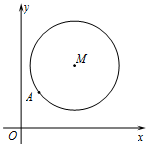
 如图,在平面直角坐标系xOy中,已知以M为圆心的圆M:x2+y2-12x-14y+60=0及其上一点A(2,4).
如图,在平面直角坐标系xOy中,已知以M为圆心的圆M:x2+y2-12x-14y+60=0及其上一点A(2,4).分析 (1)将圆M化为标准方程,求得圆心和半径,直线AM的斜率和切线的斜率,由点斜式方程即可得到所求切线的方程;
(2)由题意得OA=2$\sqrt{5}$,kOA=2,设l:y=2x+b,则圆心M到直线l的距离:d=$\frac{|5+b|}{\sqrt{5}}$,由此能求出直线l的方程;
(3)$\overrightarrow{TA}$=$\overrightarrow{PQ}$,即|$\overrightarrow{TA}$|=$\sqrt{(t-2)^{2}+{4}^{2}}$,又|$\overrightarrow{PQ}$|≤10,得t∈[2-2$\sqrt{21}$,2+2$\sqrt{21}$],对于任意t∈[2-2$\sqrt{21}$,2+2$\sqrt{21}$].欲使$\overrightarrow{TA}$=$\overrightarrow{PQ}$,只需要作直线TA的平行线,使圆心到直线的距离为$\sqrt{25-\frac{|\overrightarrow{TA}{|}^{2}}{4}}$,由此能求出实数t的取值范围.
解答 解:(1)由题意,圆M:(x-6)2+(y-7)2=25,圆心M(6,7),
则kAM=$\frac{7-4}{6-2}$=$\frac{3}{4}$,所以切线方程y-4=-$\frac{4}{3}$(x-2),即4x+3y-20=0;…(4分)
(2)由题意得OA=2$\sqrt{5}$,kOA=2,设l:y=2x+b,
则圆心M到直线l的距离d=$\frac{|12-7+b|}{\sqrt{{2}^{2}+{1}^{2}}}$=$\frac{|5+b|}{\sqrt{5}}$,…(6分)
则|BC|=2$\sqrt{{5}^{2}-{d}^{2}}$=2$\sqrt{25-\frac{(5+b)^{2}}{5}}$,
又|BC|=2$\sqrt{5}$,即2$\sqrt{25-\frac{(5+b)^{2}}{5}}$=2$\sqrt{5}$,
解得b=5或b=-15,即l:y=2x+5或y=2x-15; …(8分)
(3)$\overrightarrow{TA}$+$\overrightarrow{TP}$=$\overrightarrow{TQ}$,即$\overrightarrow{TA}$=$\overrightarrow{TQ}$-$\overrightarrow{TP}$=$\overrightarrow{PQ}$,即|$\overrightarrow{TA}$|=|$\overrightarrow{PQ}$|,
|$\overrightarrow{TA}$|=$\sqrt{(t-2)^{2}+{4}^{2}}$,
又|$\overrightarrow{PQ}$|≤10,即$\sqrt{(t-2)^{2}+{4}^{2}}$≤10,解得t∈[2-2$\sqrt{21}$,2+2$\sqrt{21}$].
对于任意t∈[2-2$\sqrt{21}$,2+2$\sqrt{21}$],欲使$\overrightarrow{TA}$=$\overrightarrow{PQ}$,
此时|$\overrightarrow{TA}$|≤10,只需要作直线TA的平行线,使圆心到直线的距离为$\sqrt{25-\frac{|\overrightarrow{TA}{|}^{2}}{4}}$.
必然与圆交于P、Q两点,此时|$\overrightarrow{TA}$|=|$\overrightarrow{PQ}$|,即$\overrightarrow{TA}$=$\overrightarrow{PQ}$,
因此实数t的取值范围为t∈[2-2$\sqrt{21}$,2+2$\sqrt{21}$].…(12分)
点评 本题考查圆的标准方程的求法,考查直线方程的求法,考查实数的取值范围的求法,是中档题,解题时要认真审题,注意圆的性质的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 消费次第 | 第1次 | 第2次 | 第3次 | 第4次 | ≥5次 |
| 收费比例 | 1 | 0.95 | 0.90 | 0.85 | 0.80 |
| 消费次第 | 第1次 | 第2次 | 第3次 | 第4次 | 第5次 |
| 频数 | 60 | 20 | 10 | 5 | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<c<b | B. | b<a<c | C. | a<b<c | D. | b<c<a |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (0,4) | C. | (3,4) | D. | (4,8] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com