
| ���Ѵε� | ��1�� | ��2�� | ��3�� | ��4�� | ��5�� |
| �շѱ��� | 1 | 0.95 | 0.90 | 0.85 | 0.80 |
| ���Ѵε� | ��1�� | ��2�� | ��3�� | ��4�� | ��5�� |
| Ƶ�� | 60 | 20 | 10 | 5 | 5 |
���� ��1�������������εĻ�Ա��40�ˣ����ݸ��ʹ�ʽp=$\frac{40}{100}$=0.4��
��2���ֱ������������Ϊ��˾��õ�����Ȼ����ƽ��ֵ���ɣ�
��3�����ݹŵ���͵ĸ���������ö�ٷ���⣮
��� �⣺��1��100λ��Ա�У������������εĻ�Ա��40�ˣ����Թ���һλ��Ա�����������εĸ���Ϊp=$\frac{40}{100}$=0.4��
��2���û�Ա��1������ʱ����˾�������Ϊ200-150=50��Ԫ����
��2 ������ʱ����˾�������Ϊ200��0.95-150=40��Ԫ����
���ԣ���˾�����η����ƽ������Ϊ$\frac{50+40}{2}=45$��Ԫ����
��3�������������εĻ�Ա�У����Ѵ����ֱ�Ϊ1��2��3��4��5�ı���Ϊ20��10��5��5=4��2��1��1������
�����8���У�����2�ε���4�ˣ���ΪA1��A2��A3��A4������3�ε���2�ˣ���ΪB1��B2������4�κ�5�εĸ���1�ˣ��ֱ���ΪC��D������ȡ2�ˣ�ȡ��A1���У�A1A2��A1A3��A1A4��A1B1��A1B2��A1C��A1D ��7�֣�
ȥ��A1��ȡ��A2���У�A2A3��A2A4��A2B1��A2B2��A2C��A2D ��6�֣�
ȥ��A1��A2��A3��A4��B1��B2����ȡ��C���У�CD ��1�֣��ܵ�ȡ����n=7+6+5+4+3+2+1=28�֣�
����ǡ��1���������ε�ȡ�����У�m=4+4+4+4=16�֣�
���ԣ����2����ǡ��1�˷����εĸ���Ϊp=$\frac{m}{n}=\frac{16}{28}=\frac{4}{7}$��
���� ������Ҫ����ŵ���ʵĸ��ʹ�ʽ�������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��17��25�� | B�� | ��9��25�� | C�� | ��8��25�� | D�� | ��9��17�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | i=i-1 | B�� | m=m2+1 | C�� | k=$\frac{-1}{k}$ | D�� | x*y=a |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��1.4��2�� | B�� | ��1��1.4�� | C�� | ��1��1.5�� | D�� | ��1.5��2�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
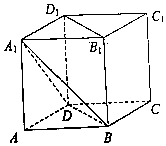 ��ͼ����������ABCD-A1B1C1D1�У�AB=2����ֱ��B1D1��ƽ�����ƽ��A1BD����ƽ����ظ����������ý�������Ϊ$\sqrt{6}$ ��
��ͼ����������ABCD-A1B1C1D1�У�AB=2����ֱ��B1D1��ƽ�����ƽ��A1BD����ƽ����ظ����������ý�������Ϊ$\sqrt{6}$ ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪��ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0�������ҽ���ֱ�ΪF1��F2��������y2=4x����ԲC����ͬ�Ľ��㣬��PΪ����������ԲC�ڵ�һ���Ľ��㣬��|PF1|=$\frac{7}{3}$��
��֪��ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0�������ҽ���ֱ�ΪF1��F2��������y2=4x����ԲC����ͬ�Ľ��㣬��PΪ����������ԲC�ڵ�һ���Ľ��㣬��|PF1|=$\frac{7}{3}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
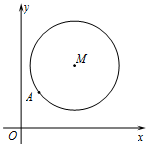 ��ͼ����ƽ��ֱ������ϵxOy�У���֪��MΪԲ�ĵ�ԲM��x2+y2-12x-14y+60=0������һ��A��2��4����
��ͼ����ƽ��ֱ������ϵxOy�У���֪��MΪԲ�ĵ�ԲM��x2+y2-12x-14y+60=0������һ��A��2��4�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x0��N | B�� | x0∉N | C�� | x0��N��x0∉N | D�� | ����ȷ�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com