
分析 先求出函数的周期,然后根据函数f(x)关于直线x=1对称则f(x)=f(2-x),利用性质化$f(\frac{1}{2})$到区间[3,4],代入f(x)=x-2求出函数值,从而得到函数值的大小关系.
解答 解:∵对任意实数x满足f(x+2)=f(x),
∴函数的周期为2,
∵f(1+x)=f(1-x),∴函数f(x)关于直线x=1对称,
∴f(x)=f(2-x),
∵当x∈[3,4]时,f(x)=x-2,
∴f($\frac{1}{2}$)=f(2-$\frac{1}{2}$)=f($\frac{3}{2}$+2)=$\frac{7}{2}$-2=$\frac{3}{2}$,
故答案为:$\frac{3}{2}$.
点评 本题主要考查了函数周期性以及奇偶性与单调性的综合,同时考查了转化能力,属于中档题.


 巧学巧练系列答案
巧学巧练系列答案 课课练江苏系列答案
课课练江苏系列答案科目:高中数学 来源: 题型:解答题
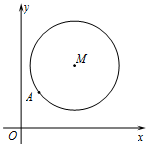 如图,在平面直角坐标系xOy中,已知以M为圆心的圆M:x2+y2-12x-14y+60=0及其上一点A(2,4).
如图,在平面直角坐标系xOy中,已知以M为圆心的圆M:x2+y2-12x-14y+60=0及其上一点A(2,4).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x0∈N | B. | x0∉N | C. | x0∈N或x0∉N | D. | 不能确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
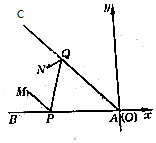 如图,∠BAC为伸入江中的半岛,AB和AC为两江岸,M处为水文站,N处为电讯局,现欲在两江岸AB和AC上各建一个水文观测点P、Q,现测得∠BAC=45°,当直角坐标系以点A为坐标原点且以直线BA为x轴时,测得M(-4,1)、N(-3,2).P、Q两点应建在何处才能使路程MPQN最短?
如图,∠BAC为伸入江中的半岛,AB和AC为两江岸,M处为水文站,N处为电讯局,现欲在两江岸AB和AC上各建一个水文观测点P、Q,现测得∠BAC=45°,当直角坐标系以点A为坐标原点且以直线BA为x轴时,测得M(-4,1)、N(-3,2).P、Q两点应建在何处才能使路程MPQN最短?查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
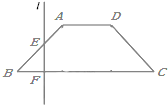 如图,已知底角为45°的等腰梯形ABCD,底边BC长为7cm,腰长为2$\sqrt{2}$cm,当一条垂直于底边BC(垂足为F)的直线l从左至右移动(与梯形ABCD有公共点)时,直线l把梯形分成两部分,令BF=x,
如图,已知底角为45°的等腰梯形ABCD,底边BC长为7cm,腰长为2$\sqrt{2}$cm,当一条垂直于底边BC(垂足为F)的直线l从左至右移动(与梯形ABCD有公共点)时,直线l把梯形分成两部分,令BF=x,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com