
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
分析 令P与A1点重合,Q与C1点重合,可判断①.当P与A1点重合时,BP与直线B1C所成的角最小,此时两异面直线夹角为60°,可判断②.根据平面OBD将四面体BDPQ可分成两个底面均为平面OBD,高之和为PQ的棱锥(其中O为上底面中心),可判断③;根据四面体BDPQ在该正方体六个面上的正投影的面积不变,可判断④.
解答 解:对于①.当P与A1点重合,Q与C1点重合时,BP⊥DQ,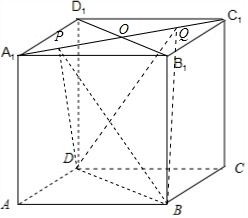 故①正确;
故①正确;
对于②.当P与A1点重合时,BP与直线B1C所成的角最小,此时两异面直线夹角为60°,故②错误.
对于③.设平面A1B1C1D1两条对角线交点为O,则易得PQ⊥平面OBD.平面OBD将四面体BDPQ可分成两个底面均为平面OBD,高之和为PQ的棱锥,故四面体BDPQ的体积一定是定值,故③正确.
对于④.四面体BDPQ在上下两个底面上的投影是对角线互相垂直且对角线长度均为1的四边形,其面积为定值.四面体BDPQ在四个侧面上的投影,均为上底为$\frac{\sqrt{2}}{2}$,下底和高均为1的梯形,其面积为定值.故四面体BDPQ在该正方体六个面上的正投影的面积的和为定值.故④正确.
综上可得:只有①③④正确.
故选:B.
点评 本题考查了综合考查了正方体的性质、空间位置关系、线面垂直的判定与性质定理、棱锥的体积计算公式、直角三角形的边角关系、异面直线所成的角,考查了推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:选择题
| A. | a<c<b | B. | b<a<c | C. | a<b<c | D. | b<c<a |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$+$\frac{1}{2}$i | B. | $\frac{1}{2}$+$\frac{1}{2}$i | C. | $\frac{1}{2}$-$\frac{1}{2}$i | D. | -$\frac{1}{2}$-$\frac{1}{2}$i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,1] | B. | (-∞,-1]∪[1,+∞) | C. | [-1,2] | D. | [3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{3}{4}$ | B. | $\frac{3}{5}$ | C. | -$\frac{4}{5}$ | D. | -$\frac{4}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com