
分析 (1)由直线l的参数方程消去参数t,能求出直线l的普通方程;在圆C的参数方程中,由sin2θ+cos2θ=1,能求出圆C的普通方程.
(2)由直线l与圆C有公共点,得到圆心C(2,0)到直线l:2x-2-2a=0的距离不大于半径,由此能求出实数a的取值范围.
解答 (本小题满分10分)选修4-4:坐标系与参数方程
解:(1)∵直线l的参数方程为$\left\{\begin{array}{l}{x=a+2t}\\{y=4t}\end{array}\right.$(t为参数),
∴消去参数t,得:x=a+$\frac{y}{2}$,整理,得:2x-y-2a=0.
∴直线l的普通方程为:2x-y-2a=0.
∵圆C的参数方程为$\left\{\begin{array}{l}x=2+cosθ\\ y=sinθ\end{array}\right.$(θ为常数),
∴$\left\{\begin{array}{l}{cosθ=x-2}\\{sinθ=y}\end{array}\right.$,
∵sin2θ+cos2θ=1,
∴圆C的普通方程为:(x-2)2+y2=1.
(2)∵直线l与圆C有公共点,
圆C:(x-2)2+y2=1的圆心为C(2,0),半径为r=1,
∴圆心C(2,0)到直线l:2x-2-2a=0的距离:
$d=\frac{{|{4-2a}|}}{{\sqrt{5}}}≤1$,
解得$\frac{4-\sqrt{5}}{2}≤a≤\frac{4+\sqrt{5}}{2}$,
∴实数a的取值范围是($\frac{4-\sqrt{5}}{2}$,$\frac{4+\sqrt{5}}{2}$).
点评 本题考查直线与圆的方程的求法,是基础题,解题时要认真审题,注意点到直线的距离公式的合理运用.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:选择题
| A. | M可能是线段AB的中点 | |
| B. | M,N 可能同时在线段BA延长线上 | |
| C. | M,N 可能同时在线段AB上 | |
| D. | M,N不可能同时在线段AB的延长线上 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 函数y=sinx,x∈[0,2π]是奇函数 | |
| B. | 函数y=2sin($\frac{π}{6}$-2x)在区间[-$\frac{π}{6},\frac{π}{3}$]上单调递减 | |
| C. | 函数y=2sin($\frac{π}{3}-2x$)-cos($\frac{π}{6}+2x$)(x∈R)的一条对称轴方程是x=$\frac{π}{6}$ | |
| D. | 函数y=sinπx•cosπx的最小正周期为2,且它的最大值为1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{6}}{4}$ | B. | $\frac{\sqrt{6}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
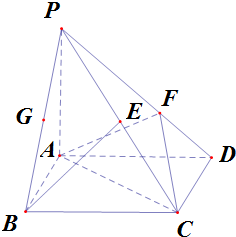 如图,四棱锥P-ABCD的底面ABCD是平行四边形,AD=2,AB=1,∠ABC=60°,PA⊥面ABCD,且PA=3,设G为PB中点,点F在线段PD上且PF=2FD.
如图,四棱锥P-ABCD的底面ABCD是平行四边形,AD=2,AB=1,∠ABC=60°,PA⊥面ABCD,且PA=3,设G为PB中点,点F在线段PD上且PF=2FD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | bc(b+c)≤8 | B. | bc(b+c)>8 | C. | 12≤abc≤24 | D. | 6≤abc≤12 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com