练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

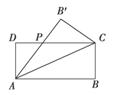
    设矩形ABCD(AB＞AD)的周长为24，把它关于AC折起来，AB折过去后交CD于点P，如图，设AB＝x，求△ADP的面积的最大值，及此时x的值．


    解：∵AB＝x，∴AD＝12－x，

    又DP＝PB′，AP＝AB′－PB′＝AB－DP，

    即AP＝x－DP，

    ∴(12－x)2＋PD2＝(x－PD)2，得PD＝12－，

    ∵AB＞AD，∴6＜x＜12，

    ∴△ADP的面积S＝AD·DP

    ＝108－6≤108－6·2＝108－72，

    当且仅当，即x＝6时取等号，

    ∴△ADP面积的最大值为108－72，此时x＝6.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知{an}为等比数列，a4＋a7＝2，a5a6＝－8，则a1＋a10＝(　　)

    A．7                                 B．5

    C．－5                               D．－7

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    x＝(a＋3)(a－5)与y＝(a＋2)(a－4)的大小关系是(　　)

    A．x>y　　　　　　　　            B．x＝y

    C．x<y                            D．不能确定

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    下列不等式一定成立的是(　　)

    A．lg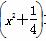＞lgx(x＞0)

    B．sinx＋≥2(x≠kπ，k∈Z)

    C．x2＋1≥2|x|(x∈R)

    D. 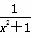＞1(x∈R)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     (1)设0<x<，求函数y＝4x(3－2x)的最大值；

    (2)已知x，y都是正实数，且x＋y－3xy＋5＝0，求xy的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若f(x)＝x2－2x－4ln x，则f′(x)＞0的解集为(　　)

    A．(0，＋∞)                      B．(－1,0)∪(2，＋∞)

    C．(2，＋∞)                      D．(－1,0)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如果关于x的不等式5x2－a≤0的正整数解是1,2,3,4，那么实数a的取值范围是(　　)

    A．80≤a＜125                     B．80＜a＜125

    C．a＜80                          D．a＞125

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设函数f(x)＝D是由x轴和曲线y＝f(x)及该曲线在点(1,0)处的切线所围成的封闭区域，则z＝x－2y在D上的最大值为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    用数学归纳法证明(n＋1)(n＋2)·…·(n＋n)＝2n·1·3·…·(2n－1)，从k到k＋1，左边需要增乘的代数式为(　　)

    A．2k＋1                           B．2(2k＋1)

    C. 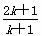                          D.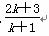

    查看答案和解析>>

    同步练习册答案