
某软件公司新开发一款学习软件,该软件把学科知识设计为由易到难共12关的闯关游戏.为了激发闯关热情,每闯过一关都奖励若干慧币(一种网络虚拟币).该软件提供了三种奖励方案:第一种,每闯过一关奖励40慧币;第二种,闯过第一关奖励4慧币,以后每一关比前一关多奖励4慧币;第三种,闯过第一关奖励0.5慧币,以后每一关比前一关奖励翻一番(即增加1倍),游戏规定:闯关者须于闯 关前任选一种奖励方案.
关前任选一种奖励方案.
(1)设闯过n(n∈N*,且n≤12)关后三种奖励方案获
 得的慧币依次为An,Bn,Cn,试求出An,Bn,Cn的表达式;
得的慧币依次为An,Bn,Cn,试求出An,Bn,Cn的表达式;
(2)如果你是一名闯关者,为了得到更多的慧币,你应如何选择奖励方案?
解:(1)第一种奖励方案闯过各关所得慧币构成常数列,∴An=40n,
第二种奖励方案闯过各关所得慧币构成首项是4,公差为4的等差数列,
∴Bn=4n+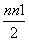 ×4=2n2+2n,
×4=2n2+2n,
第三种奖励方案闯过各关所得慧币构成首项是0.5,公比为2的等比数列,
∴Cn=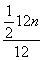 =
=
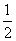 (2n
(2n -1
-1 ).
).
(2)令An>Bn,即40n>2n2+2n,解得n<19,
∵n∈N*,且 n≤12,∴An>Bn恒成立.
n≤12,∴An>Bn恒成立.
令An>Cn,即40n>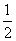 (2n-1),可得n<10,
(2n-1),可得n<10,
∴当n<10时,An最大;当10≤n≤12时, Cn>An.
综上,若我是一名闯关者,当能冲过的关数小于10时,应选用第一种奖励方案;当能冲过的关数大于等于10时,应选用第三种奖励方案.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:
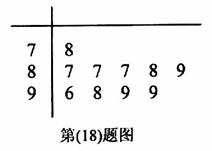
学校为测评班级学生对任课教师的满意度,采用“100分制”打分的方式来计分.现从某班学生中随机抽取10名,以下茎叶图记录了他们对某教师的满意度分数(以十位数字为茎,个位数字为叶):
规定若满意度不低于98分,测评价该教师为“优秀”.
(I)求从这10人中随机选取3人,至多有1人评价该教师是“优秀”的概率;
(II)以这10人的样本数据来估计整个班级的总体数据,若从该班任选3人,记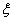 表示抽到评价该教师为“优秀”的人数,求
表示抽到评价该教师为“优秀”的人数,求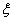 的分布列.
的分布列.
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com