
分析 (1)通过分析可知从2007年开始年处理垃圾吨量构成以5万吨为首项、1.1为公比的等比数列,分别计算出2008、2009年底的垃圾总量、相减计算即得结论;
(2)通过设到(2006+n)年底垃圾堆积量最多,利用该年处理垃圾刚超过8万吨计算即得结论;
(3)通过记s是第2006+x的垃圾总量,计算可知s=150+8x-50×1.1x,解不等式150+8x-50×1.1x<50,取x的最小正整数即得结论.
解答 解:(1)依题意,从2007年开始,年处理垃圾吨量构成以5万吨为首项、1.1为公比的等比数列,
∴到2008年垃圾总的应该是100+8×2-5-5×1.1=105.5,
2009年应该是105+8-5×1.1×1.1=106.95,
∴106.95-105.5=1.95,
即2009年底比2008年底垃圾量增加1.95;
(2)设到(2006+n)年底垃圾堆积量最多,
依题意,则该年处理垃圾刚超过8万吨,
∴5×1.1n>8,即1.1n>1.6,
解得:n>4.9,
∴n=5,2006+n=2011,
即2011年垃圾堆积量最多;
(3)记s是第2006+x的垃圾总量,
则s=100+8x-$\frac{5×(1-1.{1}^{x})}{1-1.1}$
=100+8x-50×1.1x+50
=150+8x-50×1.1x,
令s<50,即150+8x-50×1.1x<50,
整理得:50×(1+0.1)x-8x>100,
∴50×[${C}_{x}^{0}$+${C}_{x}^{1}$×0.11+${C}_{x}^{2}$×0.12+…+${C}_{x}^{x}$×0.1x]-8x>100,
计算可知,x=16,
即从2022年开始,垃圾堆积少于50万吨.
点评 本题考查函数模型的选择与应用,考查运算求解能力,注意解题方法的积累,属于中档题.


科目:高中数学 来源: 题型:解答题
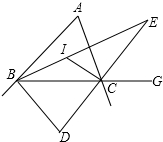 好学的小红在学完三角形的角平分线后,遇到下列4个问题,请你帮她解决,如图,在ABC中,∠BAC=50°,点I是两角B、C平分线的交点.
好学的小红在学完三角形的角平分线后,遇到下列4个问题,请你帮她解决,如图,在ABC中,∠BAC=50°,点I是两角B、C平分线的交点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | P<R<Q | B. | R<Q<P | C. | R<P<Q | D. | Q<R<P |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com