解:(1)f′(x)=3x
2-3a
若a<0则可得f′(x)≥0,不合题意
若a>0则


可得
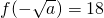
∴a=4
(II)设切点为(x
0,y
0)而f(x)=x
3-12x+2
故
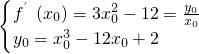
,则
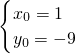
,故切线为y=-9x
由题意得
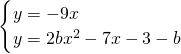
,说明函数h(x)=2bx
2+2x-3-b在区间[-1,1]上有零点
若b=0,则函数h(x)=2x-3在[-1,1]上没有零点
若a≠0,时分三种情况讨论:
①方程h(x)=0在区间[-1,1]上有重根,此时△=4(2b
2+6b+1)=0,解得
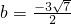
当

时,h(x)=0的重根
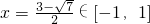
当
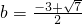
时,h(x)=0的重根
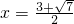
∉[-1,1]
故当方程h(x)=0在区间[-1,1]上有重根时,b=
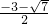
②h(x)在区间[-1,1]上只有一个零点且不是h(x)=0的重根
此时有h(-1)h(1)≤0∵h(-1)=b-5,h(1)=b-1∴(b-5)(b-1)≤0?1≤b≤5
∵当b=5时,方程h(x)=0在区间[-1,1]上有两个不同的实根
故当方程h(x)=0在区间[-1,1]上只有一个根且不是重根时,1≤b<5
③方程h(x)=0在区间[-1,1]有两个不同的实根,则
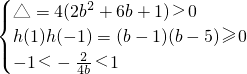
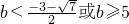
综上可得,b的取值范围
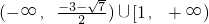
分析:(I)先对函数求导f′(x)=3x
2-3a,分a>0,f′(x)≥0,a>0则

,讨论函数的单调性,进而求解函数的极值,从而可求a
(II)由题意可求切线方程y=-9x,由
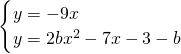
,在[-1,1]上的图象有交点,说明函数得函数h(x)=2bx
2+2x-3-b在区间[-1,1]上有零点,利用方程的实根分别问题进行求解即可
点评:本题主要考查了利用导数判断函数的单调性及求解函数的极值,导数的几何意义的应用,解决本题的关键是灵活应用方程的实根分布进行求解.



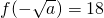 ∴a=4
∴a=4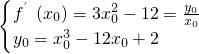 ,则
,则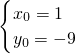 ,故切线为y=-9x
,故切线为y=-9x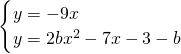 ,说明函数h(x)=2bx2+2x-3-b在区间[-1,1]上有零点
,说明函数h(x)=2bx2+2x-3-b在区间[-1,1]上有零点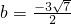
 时,h(x)=0的重根
时,h(x)=0的重根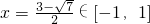
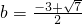 时,h(x)=0的重根
时,h(x)=0的重根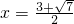 ∉[-1,1]
∉[-1,1]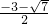
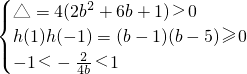
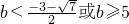
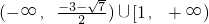
 ,讨论函数的单调性,进而求解函数的极值,从而可求a
,讨论函数的单调性,进而求解函数的极值,从而可求a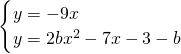 ,在[-1,1]上的图象有交点,说明函数得函数h(x)=2bx2+2x-3-b在区间[-1,1]上有零点,利用方程的实根分别问题进行求解即可
,在[-1,1]上的图象有交点,说明函数得函数h(x)=2bx2+2x-3-b在区间[-1,1]上有零点,利用方程的实根分别问题进行求解即可

 名校课堂系列答案
名校课堂系列答案 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<