
����Ŀ��ij���²�ƷͶ���г�һ��ʱ��������л����ʱ��![]() �������������۵���
�������������۵���![]() ��Ԫ����һ�����ݣ�������һ�������ݴ��������������������ɢ��ͼ����ͼ��
��Ԫ����һ�����ݣ�������һ�������ݴ��������������������ɢ��ͼ����ͼ��
|
|
|
|
|
|
|
|
|
|
|
|
|
|
����![]() ��
��![]() .
.
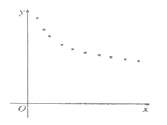
��1������ɢ��ͼ�жϣ�![]() ��
��![]() ��һ�����������۸�
��һ�����������۸�![]() ����ʱ��
����ʱ��![]() �Ļع鷽�����ͣ�������˵�����ɣ�
�Ļع鷽�����ͣ�������˵�����ɣ�
��2�������жϽ���ͱ������ݣ�����![]() ����
����![]() �Ļع鷽�̣�
�Ļع鷽�̣�
��3�����ò�Ʒ����������![]() ��������ʱ��
��������ʱ��![]() �ĺ�����ϵΪ
�ĺ�����ϵΪ![]() ��
��![]() ������ò�ƷͶ���г��ڼ�������۶���ߣ����Ϊ����Ԫ�����������������
������ò�ƷͶ���г��ڼ�������۶���ߣ����Ϊ����Ԫ�����������������
��������һ������![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ����ع�ֱ��
����ع�ֱ��![]() ��б�ʺͽؾ����С���˹��Ʒֱ�Ϊ
��б�ʺͽؾ����С���˹��Ʒֱ�Ϊ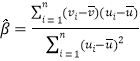 ��
��![]() .
.
���𰸡�(1)������;(2)![]() ;(3)�ò�ƷͶ���г���
;(3)�ò�ƷͶ���г���![]() ������۶���ߣ����ԼΪ
������۶���ߣ����ԼΪ![]() Ԫ.
Ԫ.
����������������1�������и�����ɢ��ͼ�����ڷ������������ݴ˿���ѡ���ع鷽�̵�����.
��2�����ݸ����Ĺ�ʽ����ع鷽�̼���.
��3�����ݻع鷽�̺�![]() �õ������۶�ĺ������䷽������������ֵ.
�õ������۶�ĺ������䷽������������ֵ.
��⣺��1����ɢ��ͼ�����ж�![]() �ʺ������۸�
�ʺ������۸�![]() ����ʱ��
����ʱ��![]() �Ļع鷽�����ͣ�
�Ļع鷽�����ͣ�
��2����![]() ���Ƚ���
���Ƚ���![]() ����
����![]() �����Իع鷽�̣�����
�����Իع鷽�̣�����![]() ��
��
��![]() ����
����![]() ����
����![]() �����Է���Ϊ
�����Է���Ϊ![]() ��
��
��![]() ����
����![]() �����Է���Ϊ
�����Է���Ϊ![]()
��3���������۶�Ϊ![]() ����
����![]()
![]()
![]() ��
��
��![]() ʱ��
ʱ��![]() ��Ԫ��
��Ԫ��
���ò�ƷͶ���г���![]() ������۶���ߣ����ԼΪ
������۶���ߣ����ԼΪ![]() Ԫ.
Ԫ.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��

![]() ������������������ѡһ������֤����
������������������ѡһ������֤����
![]() ��
��![]() ʱ����
ʱ����![]() ǡ��һ����㣻
ǡ��һ����㣻
![]() ��
��![]() ʱ����
ʱ����![]() ǡ��һ����㣻
ǡ��һ����㣻
![]() ��ͼ��ʾ��
��ͼ��ʾ��![]() ʱ
ʱ![]() ��
��![]() ��
��![]() ��
��![]() ��ͼ����ֻ��һ�����㣬��ʵ�����������������������㣬��֤������
��ͼ����ֻ��һ�����㣬��ʵ�����������������������㣬��֤������![]() ʱ��
ʱ��![]() ��
��![]() �������㣮
�������㣮
![]() ������
������![]() ǡ��4��ʵ����������
ǡ��4��ʵ����������![]() ���о���ָ��ʵ��k��ȡֵ��Χ
���о���ָ��ʵ��k��ȡֵ��Χ![]() ����֤��
����֤��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����5��ʵϰ�����䵽������ʵϰ��ÿ������1��������䷽�����У� ��
A. 240�� B. 150�� C. 180�� D. 60��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������ʽ��![]()
![]() ����
����![]() ��ֵ��
��ֵ��
![]() ����
����![]() ��
��![]() ��ֵ��
��ֵ��
![]() ������ʵ��x������ʽ
������ʵ��x������ʽ![]() ���������ʵ��a��ȡֵ��Χ��
���������ʵ��a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=x��lnx��g��x��=x2��ax��
��1������f��x��������[t��t+1]��t��0���ϵ���Сֵm��t����
��2����h��x��=g��x����f��x����A��x1 �� h��x1������B��x2 �� h��x2������x1��x2���Ǻ���h��x��ͼ�����������㣬������ ![]() ��1����ʵ��a��ȡֵ��Χ��
��1����ʵ��a��ȡֵ��Χ��
��3����x�ʣ�0��1]��ʹf��x���� ![]() ��������ʵ��a�����ֵ��
��������ʵ��a�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������ල������߾���2004��5��31�շ������µ�![]() ������ʻ��ԱѪҺ�������ƾ�������ֵ�����
������ʻ��ԱѪҺ�������ƾ�������ֵ�����![]() ���ұ�
���ұ�![]() �±��涨��������ʻ��ԱѪҺ�еľƾ��������ڻ����20����
�±��涨��������ʻ��ԱѪҺ�еľƾ��������ڻ����20����![]() �ٺ�����С��80����
�ٺ�����С��80����![]() �ٺ���Ϊ���Ƽݳ���ѪҺ�еľƾ��������ڻ����80����
�ٺ���Ϊ���Ƽݳ���ѪҺ�еľƾ��������ڻ����80����![]() �ٺ���Ϊ���Ƽݳ�
�ٺ���Ϊ���Ƽݳ�![]() �����������飬��һƿơ�ƺ�ƾ�������ѪҺ�еı仯���ɵġ�ɢ��ͼ����ͼ��
�����������飬��һƿơ�ƺ�ƾ�������ѪҺ�еı仯���ɵġ�ɢ��ͼ����ͼ��

�ú�������ģ�����£�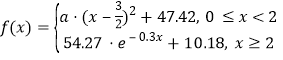 ,����֪�պù�1Сʱʱ��þƾ�����ֵΪ
,����֪�պù�1Сʱʱ��þƾ�����ֵΪ![]() ����
����![]() �ٺ���
�ٺ���![]() ���������������ش��������⣺
���������������ش��������⣺
![]() �Լ����1ƿơ�ƶ���СʱѪҺ�еľƾ������ﵽ���ֵ�����ֵ�Ƕ��٣�
�Լ����1ƿơ�ƶ���СʱѪҺ�еľƾ������ﵽ���ֵ�����ֵ�Ƕ��٣�
![]() �Լ����һƿơ�ƺ����Сʱ��ſ��Լݳ���
�Լ����һƿơ�ƺ����Сʱ��ſ��Լݳ���![]() ʱ������Сʱ����
ʱ������Сʱ����![]()
![]() �ο����ݣ�
�ο����ݣ�![]() ��
��![]() ��
��![]() ��
��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������װ��һЩ��С��ͬ��С�����к���Ϊ1��С��1��������Ϊ2��С��2��������Ϊ3��С��3������������Ϊn��С����n�����Ӵ���ȡһ���������Ϊ�������![]() ����
����![]() ����ѧ����E
����ѧ����E![]() =______________.
=______________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ⳤ��Ϊ2��������P��ABCD�У���EΪPC�е㣬������������ȷ���ǣ� �� 
A.BEƽ����PAD����ֱ��BE����PAD����Ϊ ![]()
B.BEƽ����PAD����ֱ��BE����PAD����Ϊ ![]()
C.BE��ƽ����PAD����BE��ƽ��PAD���ɽǴ��� ![]()
D.BE��ƽ����PAD����BE����PAD���ɽ�С�� ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס�����������ͬ�����¸����10��,ÿ�δ�����õĻ�����ͼ��ʾ.
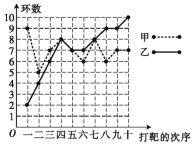
��д�±���������нǶȶ���ν�����з���.
����9�������ϵĴ��� | ƽ���� | ��λ�� | ���� | |
�� | ||||
�� |
(1)����9�������ϵĴ���(����˭�ijɼ���Щ);
(2)ƽ��������λ��(����˭�ijɼ���Щ);
(3)����(����˭�ijɼ����ȶ�);
(4)����ͼ������������л���������(����˭����DZ��).
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com