
【题目】在直角坐标系![]() 中,曲线C的参数方程为
中,曲线C的参数方程为 为参数.在以原点
为参数.在以原点![]() 为极点,为参数).在以原点
为极点,为参数).在以原点![]() 为极点,轴的正半轴为极轴的极坐标系中,直线
为极点,轴的正半轴为极轴的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求曲线C的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设![]() ,直线
,直线![]() 与曲线C交于M,N两点,求
与曲线C交于M,N两点,求![]() 的值.
的值.
科目:高中数学 来源: 题型:
【题目】近期,某公交公司与银行开展云闪付乘车支付活动,吸引了众多乘客使用这种支付方式.某线路公交车准备用20天时间开展推广活动,他们组织有关工作人员,对活动的前七天使用云闪付支付的人次数据做了初步处理,设第x天使用云闪付支付的人次为y,得到如图所示的散点图.
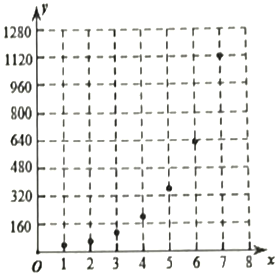
由统计图表可知,可用函数y=abx拟合y与x的关系
(1)求y关于x的回归方程;
(2)预测推广期内第几天起使用云闪付支付的人次将超过10000人次.
附:①参考数据
|
|
|
|
|
|
4 | 360 | 2.30 | 140 | 14710 | 71.40 |
表中vi=lgyi,![]() lgyi
lgyi
②参考公式:对于一组数据(u1,v1),(u2,v2)…,(un,vn),其回归直线v=α+βu的斜率和截距的最小二乘估计分别为β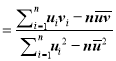 ,α
,α![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国是枇把生产大国,在对枇杷的长期栽培和选育中,形成了众多的品种.成熟的枇杷味道甜美,营养颇丰,而且中医认为枇杷有润肺、止咳、止渴的功效.因此,枇杷受到大家的喜爱.某果农调查了枇杷上市时间与卖出数量的关系,统计如表所示:

结合散点图可知,![]() 线性相关.
线性相关.
(Ⅰ)求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() =
=![]()
![]() (其中
(其中![]() ,
,![]() 用假分数表示);
用假分数表示);
(Ⅱ)计算相关系数![]() ,并说明(I)中线性回归模型的拟合效果.
,并说明(I)中线性回归模型的拟合效果.
参考数据:![]() ;
;
参考公式:回归直线方程![]() =
=![]()
![]() 中的斜率和截距的最小二乘法估计公式分别为:
中的斜率和截距的最小二乘法估计公式分别为:
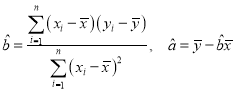 ;相关系数
;相关系数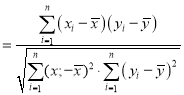
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,摩天轮的半径为50m,圆心O距地面的高度为65m.已知摩天轮按逆时针方向匀速转动,每30min转动一圈.游客在摩天轮的舱位转到距离地面最近的位置进舱.
(1)游客进入摩天轮的舱位,开始转动tmin后,他距离地面的高度为h,求h关于t的函数解析式;
(2)已知在距离地面超过40m的高度,游客可以观看到游乐场全景,那么在摩天轮转动一圈的过程中,游客可以观看到游乐场全景的时间是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com