
【题目】如图,在梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,四边形
,四边形![]() 是菱形,
是菱形,![]() .
.
(Ⅰ)求证:![]() ;
;
(Ⅱ)求二面角![]() 的平面角的正切值.
的平面角的正切值.
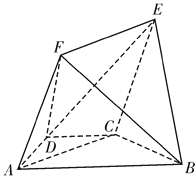
【答案】(Ⅰ)证明见解析;(Ⅱ)![]() .
.
【解析】试题分析:
(Ⅰ)由勾股定理可得![]() ,结合面面垂直的性质有
,结合面面垂直的性质有![]() .由菱形的性质可得
.由菱形的性质可得![]() ,则
,则![]() 平面
平面![]() ,
,![]() .
.
(Ⅱ)取![]() 的中点
的中点![]() ,连接
,连接![]() ,以
,以![]() 、
、![]() 、
、![]() 分别为
分别为![]() 、
、![]() 、
、![]() 轴建立空间直角坐标系,据此计算可得平面
轴建立空间直角坐标系,据此计算可得平面![]() 的法向量
的法向量![]() ,平面
,平面![]() 的法向量
的法向量![]() .
.
则二面角![]() 的平面角的余弦值
的平面角的余弦值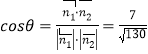 ,正切值为
,正切值为![]() .
.
试题解析:
(Ⅰ)依题意,在等腰梯形![]() 中,
中,![]() ,
,![]() ,
,
∵![]() ,∴
,∴![]() 即
即![]() ,
,
∵![]() ,∴
,∴![]() ,而
,而![]() ,∴
,∴![]() .
.
连接![]() ,∵四边形
,∵四边形![]() 是菱形,∴
是菱形,∴![]() ,
,
∴![]() ,∵
,∵![]() ,∴
,∴![]() .
.
(Ⅱ)取![]() 的中点
的中点![]() ,连接
,连接![]() ,因为四边形
,因为四边形![]() 是菱形,且
是菱形,且![]() .
.
所以由平面几何易知![]() ,∵
,∵![]() ,∴
,∴![]() .
.
故此可以![]() 、
、![]() 、
、![]() 分别为
分别为![]() 、
、![]() 、
、![]() 轴建立空间直角坐标系,各点的坐标依次为:
轴建立空间直角坐标系,各点的坐标依次为:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
设平面![]() 和平面
和平面![]() 的法向量分别为
的法向量分别为![]() ,
,![]() ,
,
∵![]() ,
,![]() .
.
∴由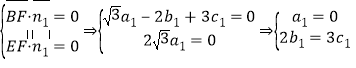 ,令
,令![]() ,则
,则![]() ,
,
同理,求得![]() .
.
∴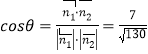 ,故二面角
,故二面角![]() 的平面角的正切值为
的平面角的正切值为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知某盒子中共有![]() 个小球,编号为
个小球,编号为![]() 号至
号至![]() 号,其中有
号,其中有![]() 个红球、
个红球、![]() 个黄球和
个黄球和![]() 个绿球,这些球除颜色和编号外完全相同.
个绿球,这些球除颜色和编号外完全相同.
(1)若从盒中一次随机取出![]() 个球,求取出的
个球,求取出的![]() 个球中恰有
个球中恰有![]() 个颜色相同的概率;
个颜色相同的概率;
(2)若从盒中逐一取球,每次取后立即放回,共取![]() 次,求恰有
次,求恰有![]() 次取到黄球的概率;
次取到黄球的概率;
(3)若从盒中逐一取球,每次取后不放回,记取完黄球所需次数为![]() ,求随机变量
,求随机变量![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某运输公司接受了向抗洪救灾地区每天送至少![]() 支援物资的任务.该公司有
支援物资的任务.该公司有![]() 辆载重
辆载重![]() 的
的![]() 型卡车与
型卡车与![]() 辆载重为
辆载重为![]() 的
的![]() 型卡车,有
型卡车,有![]() 名驾驶员,每辆卡车每天往返的次数为
名驾驶员,每辆卡车每天往返的次数为![]() 型卡车
型卡车![]() 次,
次,![]() 型卡车
型卡车![]() 次;每辆卡车每天往返的成本费
次;每辆卡车每天往返的成本费![]() 型为
型为![]() 元,
元,![]() 型为
型为![]() 元.请为公司安排一下,应如何调配车辆,才能使公司所花的成本费最低?若只安排
元.请为公司安排一下,应如何调配车辆,才能使公司所花的成本费最低?若只安排![]() 型或
型或![]() 型卡车,所花的成本费分别是多少?
型卡车,所花的成本费分别是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() ,现以极点
,现以极点![]() 为原点,极轴为
为原点,极轴为![]() 轴的非负半轴建立平面直角坐标系,曲线
轴的非负半轴建立平面直角坐标系,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
(1)求直线![]() 的直角坐标方程和曲线
的直角坐标方程和曲线![]() 的普通方程;
的普通方程;
(2)若曲线![]() 为曲线
为曲线![]() 关于直线
关于直线![]() 的对称曲线,点
的对称曲线,点![]() ,
,![]() 分别为曲线
分别为曲线![]() 、曲线
、曲线![]() 上的动点,点
上的动点,点![]() 坐标为
坐标为![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的焦距为
的焦距为![]() ,离心率为
,离心率为![]() ,圆
,圆![]() ,
,![]() 是椭圆的左右顶点,
是椭圆的左右顶点,![]() 是圆
是圆![]() 的任意一条直径,
的任意一条直径,![]() 面积的最大值为2.
面积的最大值为2.
(1)求椭圆![]() 及圆
及圆![]() 的方程;
的方程;
(2)若![]() 为圆
为圆![]() 的任意一条切线,
的任意一条切线,![]() 与椭圆
与椭圆![]() 交于两点
交于两点![]() ,求
,求![]() 的取直范围.
的取直范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线C的参数方程为
中,曲线C的参数方程为 为参数.在以原点
为参数.在以原点![]() 为极点,为参数).在以原点
为极点,为参数).在以原点![]() 为极点,轴的正半轴为极轴的极坐标系中,直线
为极点,轴的正半轴为极轴的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求曲线C的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设![]() ,直线
,直线![]() 与曲线C交于M,N两点,求
与曲线C交于M,N两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市政府为了节约生活用电,计划在本市试行居民生活用电定额管理,即确定一户居民月用电量标准a,用电量不超过a的部分按平价收费,超出a的部分按议价收费![]() 为此,政府调查了100户居民的月平均用电量
为此,政府调查了100户居民的月平均用电量![]() 单位:度
单位:度![]() ,以
,以![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分组的频率分布直方图如图所示.
分组的频率分布直方图如图所示.
![]() 根据频率分布直方图的数据,求直方图中x的值并估计该市每户居民月平均用电量
根据频率分布直方图的数据,求直方图中x的值并估计该市每户居民月平均用电量![]() 的值;
的值;
![]() 用频率估计概率,利用
用频率估计概率,利用![]() 的结果,假设该市每户居民月平均用电量X服从正态分布
的结果,假设该市每户居民月平均用电量X服从正态分布![]()
![]() 估计该市居民月平均用电量介于
估计该市居民月平均用电量介于![]() 度之间的概率;
度之间的概率;
![]() 利用
利用![]() 的结论,从该市所有居民中随机抽取3户,记月平均用电量介于
的结论,从该市所有居民中随机抽取3户,记月平均用电量介于![]() 度之间的户数为
度之间的户数为![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com