
 座落于我市红梅公园边的天宁宝塔堪称中华之最,也堪称佛塔世界之最.如图,已知天宁宝塔AB高度为150米,某大楼CD高度为90米,从大楼CD顶部C看天宁宝塔AB的张角∠ACB=45°,求天宁宝塔AB与大楼CD底部之间的距离BD.
座落于我市红梅公园边的天宁宝塔堪称中华之最,也堪称佛塔世界之最.如图,已知天宁宝塔AB高度为150米,某大楼CD高度为90米,从大楼CD顶部C看天宁宝塔AB的张角∠ACB=45°,求天宁宝塔AB与大楼CD底部之间的距离BD.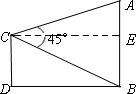 解:如图作CE⊥AB于E.
解:如图作CE⊥AB于E.| 60 |
| x |
| 90 |
| x |
| 90 |
| x |
1-
| ||
1+
|


 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:高中数学 来源: 题型:
| π |
| 6 |
| π |
| 12 |
| π |
| 6 |
| π |
| 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| FA |
| OA |
查看答案和解析>>
科目:高中数学 来源: 题型:
 在2010年的人口普查中,某市人中普查办公室为召开普查工作意见反馈会,用分层抽样的方法,从某住宅小区中抽取A、B、C、D四个年龄段的居民共50人.如图是该小区这四个年龄段的人数条形图.
在2010年的人口普查中,某市人中普查办公室为召开普查工作意见反馈会,用分层抽样的方法,从某住宅小区中抽取A、B、C、D四个年龄段的居民共50人.如图是该小区这四个年龄段的人数条形图.查看答案和解析>>
科目:高中数学 来源: 题型:
| 8 |
| 15 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com