
ФЪЖҪГжЦұҪЗЧшұкПөxOyЦР,FКЗЕЧОпПЯC:x2=2py(p>0)өДҪ№өг,MКЗЕЧОпПЯCЙПО»УЪөЪТ»ПуПЮДЪөДИОТвТ»өг,№эM,F,OИэөгөДФІөДФІРДОӘQ,өгQөҪЕЧОпПЯCөДЧјПЯөДҫаАлОӘ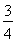 .
.
(1)ЗуЕЧОпПЯCөД·ҪіМ;
(2)КЗ·сҙжФЪөгM,К№өГЦұПЯMQУлЕЧОпПЯCПаЗРУЪөгM?ИфҙжФЪ,ЗуіцөгMөДЧшұк;ИфІ»ҙжФЪ,ЛөГчАнУЙ.
(3)ИфөгMөДәбЧшұкОӘ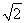 ,ЦұПЯl:y=kx+
,ЦұПЯl:y=kx+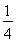 УлЕЧОпПЯCУРБҪёцІ»Н¬өДҪ»өгA,B,lУлФІQУРБҪёцІ»Н¬өДҪ»өгD,E,Зуөұ
УлЕЧОпПЯCУРБҪёцІ»Н¬өДҪ»өгA,B,lУлФІQУРБҪёцІ»Н¬өДҪ»өгD,E,Зуөұ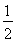 ЎЬkЎЬ2Кұ,|AB|2+|DE|2өДЧоРЎЦө.
ЎЬkЎЬ2Кұ,|AB|2+|DE|2өДЧоРЎЦө.
ЈЁ1Ј©x2=2y ЈЁ2Ј©ҙжФЪөгM(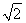 ,1) ЈЁ3Ј©
,1) ЈЁ3Ј©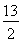
ЎҫҪвОцЎҝ
Ҫв:(1)ТАМвТвЦӘF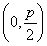 ,ФІРДQФЪПЯ¶ОOFөДҙ№ЦұЖҪ·ЦПЯy=
,ФІРДQФЪПЯ¶ОOFөДҙ№ЦұЖҪ·ЦПЯy=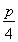 ЙП,
ЙП,
ТтОӘЕЧОпПЯCөДЧјПЯ·ҪіМОӘy=-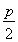 ,
,
ЛщТФ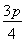 =
=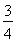 ,
,
јҙp=1.
ТтҙЛЕЧОпПЯCөД·ҪіМОӘx2=2y.
(2)јЩЙиҙжФЪөгM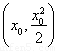 (x0>0)ВъЧгМхјю,ЕЧОпПЯCФЪөгMҙҰөДЗРПЯРұВКОӘyЎд
(x0>0)ВъЧгМхјю,ЕЧОпПЯCФЪөгMҙҰөДЗРПЯРұВКОӘyЎд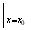 =
=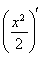
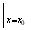 =x0,
=x0,
ЛщТФЦұПЯMQөД·ҪіМОӘy-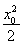 =x0(x-x0).
=x0(x-x0).
Боy=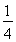 өГxQ=
өГxQ=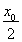 +
+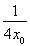 .
.
ЛщТФQЈЁ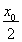 +
+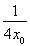 ,
,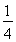 Ј©.
Ј©.
УЦ|QM|=|OQ|,
№КЈЁ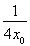 -
-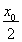 Ј©2+ЈЁ
Ј©2+ЈЁ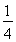 -
-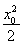 Ј©2=ЈЁ
Ј©2=ЈЁ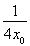 +
+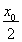 Ј©2+
Ј©2+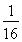 ,
,
ТтҙЛЈЁ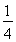 -
-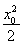 Ј©2=
Ј©2=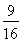 .
.
УЦx0>0,
ЛщТФx0=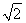 ,ҙЛКұM(
,ҙЛКұM(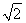 ,1).
,1).
№КҙжФЪөгM(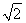 ,1),
,1),
К№өГЦұПЯMQУлЕЧОпПЯCПаЗРУЪөгM.
(3)өұx0=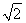 Кұ,УЙ(2)өГQЈЁ
Кұ,УЙ(2)өГQЈЁ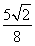 ,
,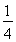 Ј©,
Ј©,
Ё‘QөД°лҫ¶ОӘr= =
=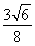 ,
,
ЛщТФЁ‘QөД·ҪіМОӘЈЁx-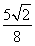 Ј©2+ЈЁy-
Ј©2+ЈЁy-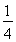 Ј©2=
Ј©2=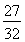 .
.
УЙ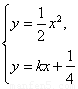
ХыАнөГ2x2-4kx-1=0.
ЙиA,BБҪөгөДЧшұк·ЦұрОӘ(x1,y1),(x2,y2),
УЙУЪҰӨ1=16k2+8>0,x1+x2=2k,x1x2=-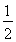 ,
,
ЛщТФ|AB|2=(1+k2)[(x1+x2)2-4x1x2]
=(1+k2)(4k2+2).
УЙ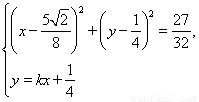
ХыАнөГ(1+k2)x2-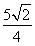 x-
x-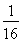 =0.
=0.
ЙиD,EБҪөгөДЧшұк·ЦұрОӘ(x3,y3),(x4,y4),
УЙУЪҰӨ2=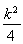 +
+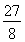 >0,x3+x4=
>0,x3+x4=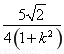 ,
,
x3x4=-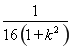 .
.
ЛщТФ|DE|2=(1+k2)[(x3+x4)2-4x3x4]
=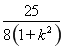 +
+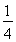 .
.
ТтҙЛ|AB|2+|DE|2=(1+k2)(4k2+2)+ 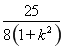 +
+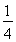 .
.
Бо1+k2=t,
УЙУЪ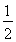 ЎЬkЎЬ2,
ЎЬkЎЬ2,
Фт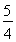 ЎЬtЎЬ5,
ЎЬtЎЬ5,
ЛщТФ|AB|2+|DE|2=t(4t-2)+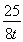 +
+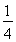
=4t2-2t+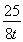 +
+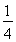 ,
,
Йиg(t)=4t2-2t+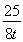 +
+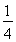 ,tЎК
,tЎК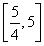 ,
,
ТтОӘgЎд(t)=8t-2-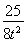 ,
,
ЛщТФөұtЎК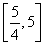 Кұ,gЎд(t)ЎЭgЎд
Кұ,gЎд(t)ЎЭgЎд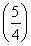 =6,
=6,
јҙәҜКэg(t)ФЪtЎК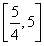 ЙПКЗФцәҜКэ,
ЙПКЗФцәҜКэ,
ЛщТФөұt=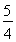 Кұ,g(t)ИЎөҪЧоРЎЦө
Кұ,g(t)ИЎөҪЧоРЎЦө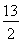 ,
,
ТтҙЛ,өұk=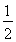 Кұ,|AB|2+|DE|2ИЎөҪЧоРЎЦө
Кұ,|AB|2+|DE|2ИЎөҪЧоРЎЦө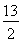 .
.


 ЖЪД©100·Цҙі№ШәЈөнҝјНхПөБРҙр°ё
ЖЪД©100·Цҙі№ШәЈөнҝјНхПөБРҙр°ё РЎС§ДЬБҰІвКФҫнПөБРҙр°ё
РЎС§ДЬБҰІвКФҫнПөБРҙр°ё
| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
| 2 |
| x2 |
| a2 |
| y2 |
| 9 |
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
 ИзНјЈ¬ФЪЖҪГжЦұҪЗЧшұкПөxOyЦРЈ¬ИсҪЗҰБәН¶ЫҪЗҰВөДЦХұЯ·ЦұрУлөҘО»ФІҪ»УЪAЈ¬BБҪөгЈ®ИфөгAөДәбЧшұкКЗ
ИзНјЈ¬ФЪЖҪГжЦұҪЗЧшұкПөxOyЦРЈ¬ИсҪЗҰБәН¶ЫҪЗҰВөДЦХұЯ·ЦұрУлөҘО»ФІҪ»УЪAЈ¬BБҪөгЈ®ИфөгAөДәбЧшұкКЗ| 3 |
| 5 |
| 12 |
| 13 |
| 16 |
| 65 |
| 16 |
| 65 |
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
| x2 |
| m |
| y2 |
| 3 |
| 1 |
| 2 |
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
| 3 | t |
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
| 16 |
| 7 |
Ійҝҙҙр°ёәНҪвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com