
在锐角△ABC中,角A,B,C的对边分别为a,b,c.已知sin(A-B)=cosC.
(1)若a=3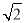 ,b=
,b=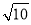 ,求c;
,求c;
(2)求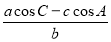 的取值范围.
的取值范围.
(1)c=4(2)(-1,1)
【解析】
试题分析:(1)由cosC=sin(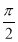 -C).结合条件可得A-B+C=
-C).结合条件可得A-B+C=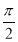 ,从而B=
,从而B=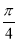 ,再利用余弦定理求出c;
,再利用余弦定理求出c;
(2)结合B=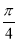 ,利用正弦定理和两角差的正弦将原式化为
,利用正弦定理和两角差的正弦将原式化为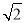 sin(2A-
sin(2A-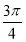 ),由A的范围可得原式的范围.
),由A的范围可得原式的范围.
试题解析:【解析】
(1)由sin(A-B)=cosC,得sin(A-B)=sin(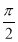 -C).
-C).
∵△ABC是锐角三角形,∴A-B=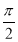 -C,即A-B+C=
-C,即A-B+C=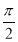 ,①
,①
又A+B+C=π,②由②-①,得B=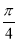 .
.
由余弦定理b2=c2+a2-2cacosB,得( )2=c2+(3
)2=c2+(3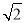 )2-2c×3
)2-2c×3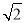 cos
cos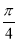 ,
,
即c2-6c+8=0,解得c=2,或c=4.
当c=2时,b2+c2-a2=( )2+22-(3
)2+22-(3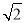 )2=-4<0,
)2=-4<0,
∴b2+c2<a2,此时A为钝角,与已知矛盾,∴c≠2.
故c=4. 6分
(2)由(1),知B=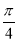 ,∴A+C=
,∴A+C=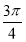 ,即C=
,即C=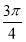 -A.
-A.
∴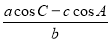 =
=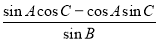 =
= =
=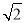 sin(2A-
sin(2A-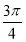 ).
).
∵△ABC是锐角三角形,∴
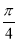 <A<
<A<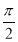 ,∴-
,∴-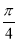 <2A-
<2A-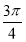 <
<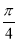 ,
,
∴-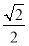 <sin(2A-
<sin(2A-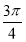 )<
)<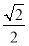 ,∴-1<
,∴-1<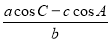 <1.
<1.
故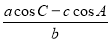 的取值范围为(-1,1). 12分
的取值范围为(-1,1). 12分
考点:正弦定理,余弦定理,三角函数性质.


科目:高中数学 来源:2016届湖北省襄阳市调研高一统一测试数学试卷(解析版) 题型:选择题
不等式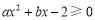 的解集为
的解集为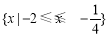 ,则( )
,则( )
A.a =-8,b =-10 B.a =-1,b = 9
C.a =-4,b =-9 D.a =-1,b = 2
查看答案和解析>>
科目:高中数学 来源:2016届湖北武汉蔡甸区第二中学高一下六科竞赛理科数学试卷(解析版) 题型:选择题
各项均为正数的等比数列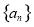 的前
的前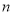 项和记为
项和记为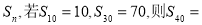 ( )
( )
A.150 B.-200 C.150或-200 D.-50或400
查看答案和解析>>
科目:高中数学 来源:2016届湖北武汉蔡甸区第二中学高一下六科竞赛数学文试卷(解析版) 题型:选择题
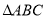 中,角
中,角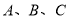 所对的边分别是
所对的边分别是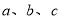 ,若角
,若角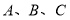 依次成等差数列,且
依次成等差数列,且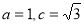 则
则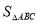 等于( ).
等于( ).
A.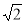 B.
B.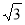 C.
C.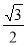 D.
D. 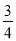
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com