
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 无数个 |
分析 设A1,A2,A3的坐标,表示出M的坐标,令|$\overrightarrow{M{A}_{1}}$+$\overrightarrow{M{A}_{2}}$+$\overrightarrow{M{A}_{3}}$|=1得出关于λ的方程,判断方程的解的个数即可得出M的位置的个数.
解答 解:以A1为原点建立坐标系,设A2(a,b),A3(m,n),则$\overrightarrow{{A}_{1}{A}_{2}}$+$\overrightarrow{{A}_{1}{A}_{3}}$=(a+m,b+n),
∴M(λ(a+m),λ(b+n)),
∴$\overrightarrow{M{A}_{1}}$=(-λ(a+m),-λ(b+n)),$\overrightarrow{M{A}_{2}}$=(a-λ(a+m),b-λ(b+n)),$\overrightarrow{M{A}_{3}}$=(m-λ(a+m),n-λ(b+n)),
∴$\overrightarrow{M{A}_{1}}$+$\overrightarrow{M{A}_{2}}$+$\overrightarrow{M{A}_{3}}$=((1-3λ)(a+m),(1-3λ)(b+n)),
∵$\overrightarrow{M{A}_{1}}$+$\overrightarrow{M{A}_{2}}$+$\overrightarrow{M{A}_{3}}$是单位向量,
∴(1-3λ)2[(a+m)2+(b+n)2]=1,
∵A1,A2,A3为平面上三个不共线的三点,∴(a+m)2+(b+n)2>0.
显然λ有两解,故满足条件的M有两个.
故选:C.
点评 本题考查令平面向量的线性运算,坐标运算,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
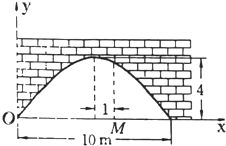 有一个抛物线形的拱形桥洞,桥洞离水面的最大高度为 4m,跨度为 10m,把它的图形放在如图所示直角坐标系中.
有一个抛物线形的拱形桥洞,桥洞离水面的最大高度为 4m,跨度为 10m,把它的图形放在如图所示直角坐标系中.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若a>b,c>d,则ac>bd | B. | 若 ac<bc,则a<b | ||
| C. | 若a>b,c>d,则a-c>b-d | D. | 若ac2<bc2,则a<b |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[{0,\frac{π}{6}}]$ | B. | $[{\frac{π}{6},\frac{2π}{3}}]$ | C. | $[{\frac{2π}{3},π}]$ | D. | $[{0,\frac{π}{6}}]$和$[{\frac{2π}{3},π}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com