

 =
= (78+79+81+84+93+95)=85
(78+79+81+84+93+95)=85 =
= (75+80+83+85+92+95)=85
(75+80+83+85+92+95)=85 [(78-85)2+(79-85)2+(81-85)2+
[(78-85)2+(79-85)2+(81-85)2+
 [(75-85)2+(80-85)2+(83-85)2+
[(75-85)2+(80-85)2+(83-85)2+
 =
= ,S甲2<S乙2
,S甲2<S乙2 .
. k=0、1、2、3
k=0、1、2、3
 .
.

科目:高中数学 来源: 题型:
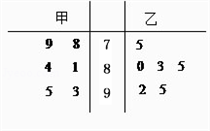
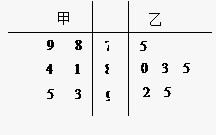 为从甲、乙两名运动员中选拔一人参加2010年广州亚运会跳水项目,对甲、乙两名运动员进行培训.现分别从他们在培训期间参加的若干次预赛成绩中随机抽取6次,得出茎叶图如如图所示
为从甲、乙两名运动员中选拔一人参加2010年广州亚运会跳水项目,对甲、乙两名运动员进行培训.现分别从他们在培训期间参加的若干次预赛成绩中随机抽取6次,得出茎叶图如如图所示查看答案和解析>>
科目:高中数学 来源:2012年人教A版高中数学必修三2.2用样本估计总体练习卷(二)(解析版) 题型:解答题
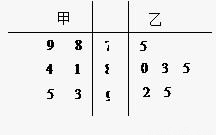
为从甲、乙两名运动员中选拔一人参加2010年广州亚运会跳水项目,对甲、乙两名运动员进行培训.现分别从他们在培训期间参加的若干次预赛成绩中随机抽取6次,得出茎叶图如图所示.
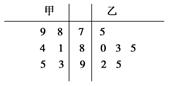
从平均成绩及发挥稳定性的角度考虑,你认为选派哪名运动员合适?
查看答案和解析>>
科目:高中数学 来源:黑龙江省模拟题 题型:解答题
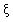 ,求ε的分布列及数学期望E
,求ε的分布列及数学期望E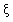 .
.
查看答案和解析>>
科目:高中数学 来源:2010年福建省漳州一中高三质量检查数学试卷(理科)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com