
“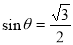 ”是“
”是“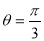 ”的( )
”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
科目:高中数学 来源:[同步]2014年苏教版必修三 3.4互斥事件练习卷(解析版) 题型:?????
从甲和乙等五名志愿者者随机抽取两人到社区服务,则甲、乙二人至少有一人未被抽中的概率为( )
A.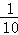 B.
B.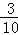 C.
C. D.
D.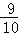
查看答案和解析>>
科目:高中数学 来源:2014-2015学年上海市闸北区高三上学期期末练习理科数学试卷(解析版) 题型:解答题
请仔细阅读以下材料:
已知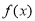 是定义在
是定义在 上的单调递增函数.
上的单调递增函数.
求证:命题“设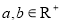 ,若
,若 ,则
,则 ”是真命题.
”是真命题.
证明 :因为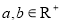 ,由
,由 得
得 .
.
又因为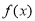 是定义在
是定义在 上的单调递增函数,
上的单调递增函数,
于是有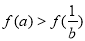 . ①
. ①
同理有 . ②
. ②
由① + ②得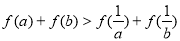 .
.
故,命题“设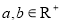 ,若
,若 ,则
,则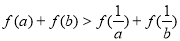 ”是真命题.
”是真命题.
请针对以上阅读材料中的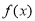 ,解答以下问题:
,解答以下问题:
(1)试用命题的等价性证明:“设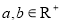 ,若
,若 ,则:
,则: ”是真命题;
”是真命题;
(2)解关于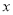 的不等式
的不等式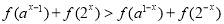 (其中
(其中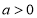 ).
).
查看答案和解析>>
科目:高中数学 来源:2014-2015学年重庆市高一上学期第三次定时练习数学试卷(解析版) 题型:解答题
(本题满分13分)已知集合 ,
, ,
,
(1)若 ,求
,求 ;
;
(2)若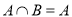 ,求实数
,求实数 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源:2014-2015学年重庆市高一上学期第三次定时练习数学试卷(解析版) 题型:选择题
定义在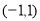 上的函数
上的函数 ;当
;当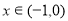 时,
时,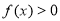 ,若
,若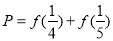 ,
,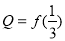 ,
,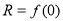 ,则P,Q,R的大小关系为( )
,则P,Q,R的大小关系为( )
A. Q>P>R B. P>Q>R C. R>Q>P D. R>P>Q
查看答案和解析>>
科目:高中数学 来源:2014-2015学年云南德宏州芒市高一上学期期末考试数学试卷(解析版) 题型:解答题
已知函数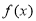 是定义域在
是定义域在 上的不恒为零的函数,且对于任意非零实数
上的不恒为零的函数,且对于任意非零实数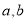 满足
满足 .
.
(1)求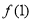 与
与 的值;
的值;
(2)判断并证明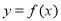 的奇偶性;
的奇偶性;
(3)若函数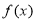 在
在 上单调递减,求不等式
上单调递减,求不等式 的解集.
的解集.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年山东省潍坊市高一上学期10月月考数学试卷(解析版) 题型:解答题
(本小题满分14分)已知奇函数
(1)求实数m的值,并在给出的直角坐标系中画出 的图象;
的图象;
(2)若函数f(x)在区间[-1,a-2]上单调递增,试确定a的取值范围
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江西省赣州市北校高二1月月考文科数学试卷(解析版) 题型:解答题
已知椭圆 的离心率为
的离心率为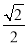 ,且过点
,且过点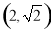
(1)求椭圆的标准方程:
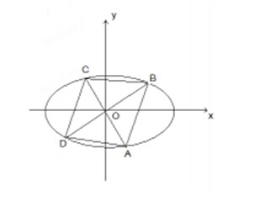 (2)四边形ABCD的顶点在椭圆上,且对角线AC,BD过原点O,若
(2)四边形ABCD的顶点在椭圆上,且对角线AC,BD过原点O,若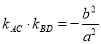
①求 的最值:
的最值:
②求证:四边形ABCD的面积为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com