
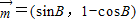 与向量
与向量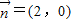 夹角的余弦角为
夹角的余弦角为 .
.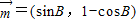 与向量
与向量 夹角的余弦角为
夹角的余弦角为 .我们可以构造一个关于角B的三角方程,解方程后,根据B为△ABC的内角,易得到角B的大小.
.我们可以构造一个关于角B的三角方程,解方程后,根据B为△ABC的内角,易得到角B的大小.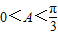 结合正弦型函数的性质,易得sinA+sinC的取值范围.
结合正弦型函数的性质,易得sinA+sinC的取值范围. (2分)
(2分)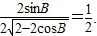 ∴2cos2B-cosB-1=0.
∴2cos2B-cosB-1=0.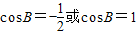 (舍)∵0<B<π∴
(舍)∵0<B<π∴ (6分)
(6分)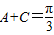
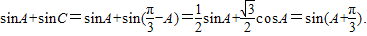 (9分)
(9分)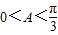 ,∴
,∴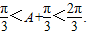
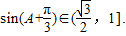 即
即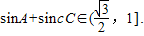 (13分)
(13分)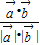 这是由向量的数量积表示夹角一唯一公式,也是利用向量求角的唯一公式,希望大家牢固掌握,熟练应用.
这是由向量的数量积表示夹角一唯一公式,也是利用向量求角的唯一公式,希望大家牢固掌握,熟练应用. 

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
| x2 |
| 16 |
| y2 |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| PA |
| PB |
| PC |
| 0 |
| AB |
| AC |
| AP |
| A、3 | ||
B、
| ||
| C、2 | ||
| D、8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com