

分析 模拟执行程序框图,可得其功能是分段函数y=$\left\{\begin{array}{l}{(a-2)x}&{x<2}\\{(\frac{1}{2})^{x}-1}&{x≥2}\end{array}\right.$单调递减,求参数a的范围
解答 解:由程序框图,可得其功能是求函数y=$\left\{\begin{array}{l}{(a-2)x}&{x<2}\\{(\frac{1}{2})^{x}-1}&{x≥2}\end{array}\right.$的值,
∵输出的y随着输入的x的增大而减小即输出的函数y单调递减,
∴$\left\{\begin{array}{l}{a-2<0}\\{2(a-2)≥(\frac{1}{2})^{2}-1}\end{array}\right.$,
解可得,$\frac{13}{8}≤a<2$,
故答案为:$[\frac{13}{8},2)$.
点评 本题考查了选择结构的程序框图,解题的关键是分段函数单调性的应用.


科目:高中数学 来源: 题型:解答题
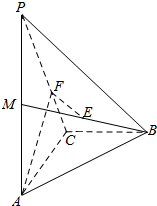 如图,在四面体P-ABC中,PA⊥面ACB,BC⊥AC,M是PA的中点,E是BM的中点,AC=2,PA=4,F是线段PC上的点,且EF∥面ACB.
如图,在四面体P-ABC中,PA⊥面ACB,BC⊥AC,M是PA的中点,E是BM的中点,AC=2,PA=4,F是线段PC上的点,且EF∥面ACB.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$,右顶点为(2,0),离心率为$\frac{{\sqrt{3}}}{2}$,直线l1:y=kx+m(k≠0,m≠0)与椭圆C相交于不同的两点A,B,过AB的中点M作垂直于l1的直线l2,设l2与椭圆C相交于不同的两点C,D,且CD的中点为N.
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$,右顶点为(2,0),离心率为$\frac{{\sqrt{3}}}{2}$,直线l1:y=kx+m(k≠0,m≠0)与椭圆C相交于不同的两点A,B,过AB的中点M作垂直于l1的直线l2,设l2与椭圆C相交于不同的两点C,D,且CD的中点为N.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个观测点C与D,测得∠BCD=15°,∠BDC=30°,CD=30米,并在C测得塔顶A的仰角为60°,则塔的高度AB为( )
如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个观测点C与D,测得∠BCD=15°,∠BDC=30°,CD=30米,并在C测得塔顶A的仰角为60°,则塔的高度AB为( )| A. | 15$\sqrt{2}$米 | B. | 15$\sqrt{3}$米 | C. | 15($\sqrt{3}$+1)米 | D. | 15$\sqrt{6}$米 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| PM 2.5日均值(微克/立方米) | [25,35] | (35,45] | (45,55] | (55,65] | (65,75] | (75,85] |
| 频数 | 3 | 1 | 1 | 1 | 1 | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在正方体ABCD一A1B1C1D1中,AB=3,CE=2EC1.
如图,在正方体ABCD一A1B1C1D1中,AB=3,CE=2EC1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com