
| A、M∈a∈α |
| B、M∈a⊆α |
| C、M⊆a⊆α |
| D、M⊆a∈α |
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
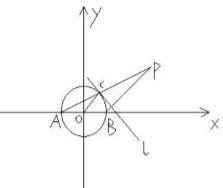 已知A,B是⊙0:x2+y2=4与x轴的两个交点,C是⊙O上异于点A,B的任意一点,过点B作直线l的垂线BP,且与AC的延长线交于点P,求点P的轨迹方程.
已知A,B是⊙0:x2+y2=4与x轴的两个交点,C是⊙O上异于点A,B的任意一点,过点B作直线l的垂线BP,且与AC的延长线交于点P,求点P的轨迹方程.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,E、F分别是三棱锥P-ABC的棱AP、BC的中点,PC=10,AB=6,EF=7,则异面直线AB与PC所成的角为( )
如图,E、F分别是三棱锥P-ABC的棱AP、BC的中点,PC=10,AB=6,EF=7,则异面直线AB与PC所成的角为( )| A、30° | B、60° |
| C、0° | D、120° |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
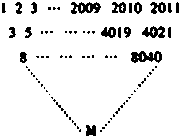 给定三角形数表如图所示,其中第一行各数依次是1,2,3,…,2009,2010,2011,从第二行起,每个数分别等于它上面一行左、右两数之和,设第i行第j个数为f(i,j)(i,j∈N*,i+j≤2012),则:f(8,1)=
给定三角形数表如图所示,其中第一行各数依次是1,2,3,…,2009,2010,2011,从第二行起,每个数分别等于它上面一行左、右两数之和,设第i行第j个数为f(i,j)(i,j∈N*,i+j≤2012),则:f(8,1)=查看答案和解析>>
科目:高中数学 来源: 题型:
| 男生 | 女生 | 合计 | |
| 收看 | 10 | ||
| 不收看 | 8 | ||
| 合计 | 30 |
| P(k2>k0) | 0.100 | 0.050 | 0.010 |
| k0 | 2.706 | 3.841 | 6.635 |
| 8 |
| 15 |
| n(ad-bc)2 |
| (a+b)(a+c)(c+d)(b+d) |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、若m∥α,n∥β,α⊥β,则m⊥n |
| B、若α∥β,m?β,m∥α,则m∥β |
| C、若α⊥β,m⊥α,则m∥β |
| D、若α⊥β,β⊥γ,则α⊥γ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com