
分析 分N=∅和N≠∅两种情况进行讨论,根据集合包含关系的判断和应用,分别求出满足条件的m值,并写成集合的形式即可得到答案.
解答 解:解:∵M={x|2x2-5x-3=0}={-$\frac{1}{2}$,3}
又∵N⊆M,
若N=∅,则m=0;
若N≠∅,则N={-$\frac{1}{2}$},或N={3},
即m=-2或m=$\frac{1}{3}$
故满足条件的实数m∈{0,-2,$\frac{1}{3}$}.
故答案为:{0,-2,$\frac{1}{3}$}.
点评 本题考查的知识点是集合的包含关系判断及应用,本题有两个易错点,一是忽N=∅的情况,二是忽略题目要求求满足条件的实数m的取值集合,而把答案没用集合形式表示.


科目:高中数学 来源: 题型:选择题
| A. | -$\frac{3}{10}$ | B. | $\frac{3}{10}$ | C. | -$\frac{2}{5}$ | D. | $\frac{2}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 7 | B. | 11 | C. | 14 | D. | 28 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,凸五面体ABCED中,DA⊥平面ABC,EC⊥平面ABC,AC=AD=AB=1,BC=$\sqrt{2}$,F为BE的中点.
如图所示,凸五面体ABCED中,DA⊥平面ABC,EC⊥平面ABC,AC=AD=AB=1,BC=$\sqrt{2}$,F为BE的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
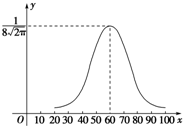 某县10000名学生的某次数学考试成绩X服从正态分布,其密度函数曲线如图,则成绩X位于区间(52,68]的人数大约是6820.
某县10000名学生的某次数学考试成绩X服从正态分布,其密度函数曲线如图,则成绩X位于区间(52,68]的人数大约是6820.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com