
【题目】已知函数![]() (
(![]() ).
).
(Ⅰ)若函数![]() 在
在![]() 处的切线平行于直线
处的切线平行于直线![]() ,求实数
,求实数![]() 的值;
的值;
(Ⅱ)讨论![]() 在
在![]() 上的单调性;
上的单调性;
(Ⅲ)若存在![]() ,使得
,使得![]() 成立,求
成立,求![]() 的取值范围.
的取值范围.
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:高中数学 来源: 题型:
【题目】如图所示,直线PQ与⊙O切于点A,AB是⊙O的弦,∠PAB的平分线AC交⊙O于点C,连接CB,并延长与直线PQ相交于Q点.
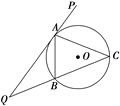
(1)求证:QC·AC=QC2-QA2;
(2)若AQ=6,AC=5,求弦AB的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图:椭圆![]() 与双曲线
与双曲线![]() 有相同的焦点
有相同的焦点![]() 、
、![]() ,它们在
,它们在![]() 轴右侧有两个交点
轴右侧有两个交点![]() 、
、![]() ,满足
,满足![]() .将直线
.将直线![]() 左侧的椭圆部分(含
左侧的椭圆部分(含![]() ,
, ![]() 两点)记为曲线
两点)记为曲线![]() ,直线
,直线![]() 右侧的双曲线部分(不含
右侧的双曲线部分(不含![]() ,
, ![]() 两点)记为曲线
两点)记为曲线![]() .以
.以![]() 为端点作一条射线,分别交
为端点作一条射线,分别交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() (点
(点![]() 在第一象限),设此时
在第一象限),设此时![]() .
.
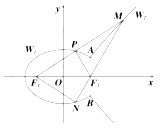
(1)求![]() 的方程;
的方程;
(2)证明: ![]() ,并探索直线
,并探索直线![]() 与
与![]() 斜率之间的关系;
斜率之间的关系;
(3)设直线![]() 交
交![]() 于点
于点![]() ,求
,求![]() 的面积
的面积![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AB为圆柱的轴,CD为底面直径,E为底面圆周上一点,AB=1,CD=2,CE=DE.
求(1)三棱锥A﹣CDE的全面积;
(2)点D到平面ACE的距离.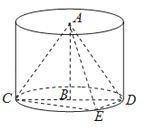
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为迎接2017年“双![]() ”,“双
”,“双![]() ”购物狂欢节的来临,某青花瓷生产厂家计划每天生产汤碗、花瓶、茶杯这三种瓷器共
”购物狂欢节的来临,某青花瓷生产厂家计划每天生产汤碗、花瓶、茶杯这三种瓷器共![]() 个,生产一个汤碗需
个,生产一个汤碗需![]() 分钟,生产一个花瓶需
分钟,生产一个花瓶需![]() 分钟,生产一个茶杯需
分钟,生产一个茶杯需![]() 分钟,已知总生产时间不超过
分钟,已知总生产时间不超过![]() 小时.若生产一个汤碗可获利润
小时.若生产一个汤碗可获利润![]() 元,生产一个花瓶可获利润
元,生产一个花瓶可获利润![]() 元,生产一个茶杯可获利润
元,生产一个茶杯可获利润![]() 元.
元.
(1)使用每天生产的汤碗个数![]() 与花瓶个数
与花瓶个数![]() 表示每天的利润
表示每天的利润![]() (元);
(元);
(2)怎样分配生产任务才能使每天的利润最大,最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据气象中心观察和预测:发生于M地的沙尘暴一直向正南方向移动,其移动速度v(km/h)与时间t(h)的函数图象如图所示,过线段OC上一点T(t,0)作横轴的垂线l,梯形OABC在直线l左侧部分的面积即为t(h)内沙尘暴所经过的路程s(km).
(1)当t=4时,求s的值;
(2)将s随t变化的规律用数学关系式表示出来;
(3)若N城位于M地正南方向,且距M地650km,试判断这场沙尘暴是否会侵袭到N城,如果会,在沙尘暴发生后多长时间它将侵袭到N城?如果不会,请说明理由.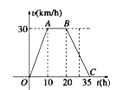
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a<1,集合A={x|x<a﹣2或x>﹣a},集合B={x|cos(xπ)=1},全集U=R.
(1)当a=0时,求(UA)∩B;
(2)若(UA)∩B恰有2个元素,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com