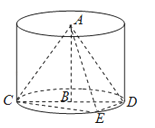
【题目】如图，AB为圆柱的轴，CD为底面直径，E为底面圆周上一点，AB=1，CD=2，CE=DE．
求（1）三棱锥A﹣CDE的全面积；
（2）点D到平面ACE的距离．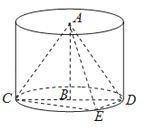
【答案】解：（1）∵AB为圆柱的轴，CD为底面直径，E为底面圆周上一点，AB=1，CD=2，CE=DE，
∴AD=
=
，∠CED=90°，
∴DE=CE==AC=AD=AE，
∴三棱锥A﹣CDE的全面积：
S=S△CDE+S△ACD+S△ACE+S△ADE
=
（X+2×1+XXsin600+XXsin600）
=2+
．
（2）设点D到平面ACE的距离为h，
由VA﹣CDE=VD﹣ACE ， 得
，
∴h=
=
=
．
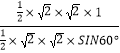【解析】（1）先求出AD= ， ∠CED=90°，DE=CE==AC=AD=AE，由此能求出三棱锥A﹣CDE的全面积．
（2）设点D到平面ACE的距离为h，由VA﹣CDE=VD﹣ACE ， 能求出点D到平面ACE的距离．
科目：高中数学 来源： 题型：
【题目】下列函数f（x）与g（x）相等的一组是（ ）
A.f（x）=x﹣1，g（x）=
﹣1
B.f（x）=x2 ， g（x）=（
）4
C.f（x）=log2x2 ， g（x）=2log2x
D.f（x）=tanx，g（x）=
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】（本小题满分13分）已知函数
（
为常数，
）
（1）若
是函数
的一个极值点，求
的值；
（2）求证：当
时，
在
上是增函数；
（3）若对任意的
，总存在
，使不等式
成立，求正实数
的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知公差大于零的等差数列
的前
项和为
，且
，
．
（1）求数列的通项公式；
（2）若数列
是等差数列，且
，求非零常数
的值．
（3）设
，
为数列
的前
项和，是否存在正整数
，使得
对任意的
均成立？若存在，求出
的最小值；若不存在，请说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知下图中，四边形 ABCD是等腰梯形， 
， 
，O、Q分别为线段AB、CD的中点，OQ与EF的交点为P，OP=1，PQ=2，现将梯形ABCD沿EF折起，使得
，连结AD、BC，得一几何体如图所示．
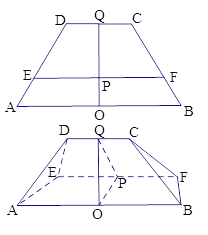
(Ⅰ)证明：平面ABCD
平面ABFE；
(Ⅱ)若上图中， 
，CD=2，求平面ADE与平面BCF所成锐二面角的余弦值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
