
【题目】已知f(x)=|x+1|+|x-1|,不等式f(x)<4的解集为M.
(1)求M.
(2)当a,b∈M时,证明:2|a+b|<|4+ab|.
科目:高中数学 来源: 题型:
【题目】某手机卖场对市民进行国产手机认可度的调查,随机抽取100名市民,按年龄(单位:岁)进行统计的频数分布表和频率分布直方图如图:
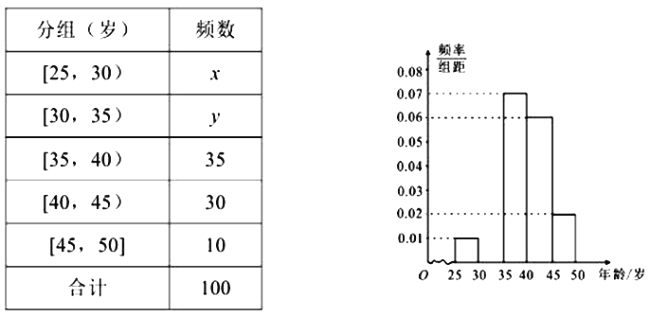
(Ⅰ)求频率分布表中![]() ,
,![]() 的值,并补全频率分布直方图;
的值,并补全频率分布直方图;
(Ⅱ)在抽取的这100名市民中,按年龄进行分层抽样,抽取20人参加国产手机用户体验问卷调查,现从这20人中随机选取2人各赠送精美礼品一份,设这2名市民中年龄在![]() 内的人数
内的人数![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从高二年级学生中随机抽取60名学生,将其期中考试的政治成绩(均为整数)分成六段: ![]() ,
, ![]() ,
, ![]() ,…
,…![]() 后得到如下频率分布直方图.
后得到如下频率分布直方图.
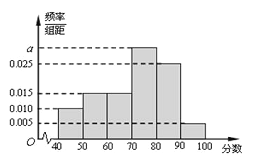
(1)根据频率分布直方图,估计该校高二年级学生期中考试政治成绩的中位数(精确到0.1)、众数、平均数;
(2)用分层抽样的方法抽取一个容量为20的样本,求各分数段抽取的人数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在几何体ABDCE中,AB=AD,AE⊥平面ABD,M为线段BD的中点,MC∥AE,AE=MC.
(1)求证:平面BCD⊥平面CDE;
(2)若N为线段DE的中点,求证:平面AMN∥平面BEC.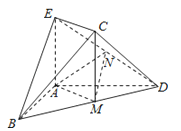
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AB为圆柱的轴,CD为底面直径,E为底面圆周上一点,AB=1,CD=2,CE=DE.
求(1)三棱锥A﹣CDE的全面积;
(2)点D到平面ACE的距离.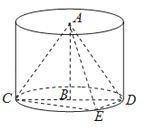
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂拟造一座平面为长方形,面积为![]() 的三级污水处理池.由于地形限制,长、宽都不能超过
的三级污水处理池.由于地形限制,长、宽都不能超过![]() ,处理池的高度一定.如果池的四周墙壁的造价为
,处理池的高度一定.如果池的四周墙壁的造价为![]() 元
元![]() ,中间两道隔墙的造价为
,中间两道隔墙的造价为![]() 元
元![]() ,池底的造价为
,池底的造价为![]() 元
元![]() ,则水池的长、宽分別为多少米时,污水池的造价最低?最低造价为多少元?
,则水池的长、宽分別为多少米时,污水池的造价最低?最低造价为多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的是一个几何体的直观图和三视图(其中正视图为直角梯形,俯视图为正方形,侧视图为直角三角形).
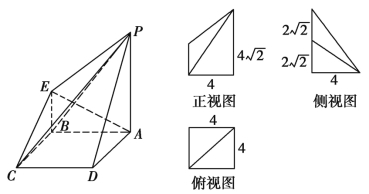
(1)求四棱锥P-ABCD的体积;
(2)若G为BC上的动点,求证:AE⊥PG.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com