
【题目】如图,在几何体ABDCE中,AB=AD,AE⊥平面ABD,M为线段BD的中点,MC∥AE,AE=MC.
(1)求证:平面BCD⊥平面CDE;
(2)若N为线段DE的中点,求证:平面AMN∥平面BEC.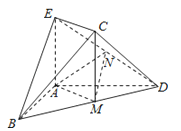
【答案】证明:(1)∵AB=AD,M为线段BD的中点,∴AM⊥BD.
∵AE⊥平面ABD,MC∥AE,∴MC⊥平面ABD.
∴MC⊥AM,∴AM⊥平面CBD.
又MC∥AE,MC=AE,∴四边形AMCE为平行四边形,
∴EC∥AM,∴EC⊥平面CBD,
∴平面BCD⊥平面CDE.
(2)∵M为BD中点,N为ED中点,
∴MN∥BE
由(1)知,EC∥AM且AM∩MN=M,BE∩EC=E,
∴平面AMN∥平面BEC.
【解析】(1)先证明AM⊥BD,MC⊥AM,从而AM⊥平面CBD,再由EC⊥平面CBD,能证明平面BCD⊥平面CDE.
(2)由三角形中位线定理得MN∥BE,再由EC∥AM,能证明平面AMN∥平面BEC.
【考点精析】认真审题,首先需要了解直线与平面平行的判定(平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行),还要掌握直线与平面垂直的性质(垂直于同一个平面的两条直线平行)的相关知识才是答题的关键.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 与y轴的正半轴相交于点M,且椭圆E上相异两点A、B满足直线MA,MB的斜率之积为
与y轴的正半轴相交于点M,且椭圆E上相异两点A、B满足直线MA,MB的斜率之积为![]() .
.
(Ⅰ)证明直线AB恒过定点,并求定点的坐标;
(Ⅱ)求三角形ABM的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在长方体ABCD﹣A1B1C1D1中,AB=![]() , BC=AA1=1,点M为AB1的中点,点P为对角线AC1上的动点,点Q为底面ABCD上的动点(点P、Q可以重合),则MP+PQ的最小值为( )
, BC=AA1=1,点M为AB1的中点,点P为对角线AC1上的动点,点Q为底面ABCD上的动点(点P、Q可以重合),则MP+PQ的最小值为( )
A.![]()
B.![]()
C.![]()
D.1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】潍坊文化艺术中心的观光塔是潍坊市的标志性建筑,某班同学准备测量观光塔![]() 的高度
的高度![]() (单位:米),如图所示,垂直放置的标杆
(单位:米),如图所示,垂直放置的标杆![]() 的高度
的高度![]() 米,已知
米,已知![]() ,
, ![]() .
.
(1)该班同学测得![]() 一组数据:
一组数据: ![]() ,请据此算出
,请据此算出![]() 的值;
的值;
(2)该班同学分析若干测得的数据后,发现适当调整标杆到观光塔的距离![]() (单位:米),使
(单位:米),使![]() 与
与![]() 的差较大,可以提高测量精确度,若观光塔高度为136米,问
的差较大,可以提高测量精确度,若观光塔高度为136米,问![]() 为多大时,
为多大时, ![]() 的值最大?
的值最大?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为选拔选手参加“中国谜语大会”,某中学举行了一次“谜语大赛”活动.为了了解本次竞赛学生的成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100分)作为样本(样本容量为![]() )进行统计.按照
)进行统计.按照![]() ,
, ![]() ,
, ![]() ,
, ![]() 的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在
的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在![]() ,
, ![]() 的数据).
的数据).
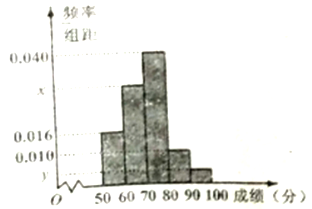

(Ⅰ)求样本容量![]() 和频率分布直方图中的
和频率分布直方图中的![]() ,
, ![]() 的值;
的值;
(Ⅱ)分数在![]() 的学生设为一等奖,获奖学金500元;分数在
的学生设为一等奖,获奖学金500元;分数在![]() 的学生设为二等奖,获奖学金200元.已知在样本中,获一、二等奖的学生中各有一名男生,则从剩下的女生中任取三人,求奖学金之和大于600的概率.
的学生设为二等奖,获奖学金200元.已知在样本中,获一、二等奖的学生中各有一名男生,则从剩下的女生中任取三人,求奖学金之和大于600的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com