
【题目】为选拔选手参加“中国谜语大会”,某中学举行了一次“谜语大赛”活动.为了了解本次竞赛学生的成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100分)作为样本(样本容量为![]() )进行统计.按照
)进行统计.按照![]() ,
, ![]() ,
, ![]() ,
, ![]() 的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在
的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在![]() ,
, ![]() 的数据).
的数据).
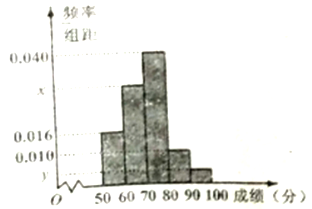

(Ⅰ)求样本容量![]() 和频率分布直方图中的
和频率分布直方图中的![]() ,
, ![]() 的值;
的值;
(Ⅱ)分数在![]() 的学生设为一等奖,获奖学金500元;分数在
的学生设为一等奖,获奖学金500元;分数在![]() 的学生设为二等奖,获奖学金200元.已知在样本中,获一、二等奖的学生中各有一名男生,则从剩下的女生中任取三人,求奖学金之和大于600的概率.
的学生设为二等奖,获奖学金200元.已知在样本中,获一、二等奖的学生中各有一名男生,则从剩下的女生中任取三人,求奖学金之和大于600的概率.
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
以直角坐标系![]() 的原点为极点,
的原点为极点, ![]() 轴的非负半轴为极轴建立极坐标系,且两坐标系有相同的长度单位.已知点
轴的非负半轴为极轴建立极坐标系,且两坐标系有相同的长度单位.已知点![]() 的极坐标为
的极坐标为![]() ,
, ![]() 是曲线
是曲线![]() :
: ![]() 上任意一点,点
上任意一点,点![]() 满足
满足![]() ,设点
,设点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(Ⅰ)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)若过点![]() 的直线
的直线![]() 的参数方程
的参数方程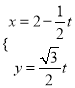 (
(![]() 为参数),且直线
为参数),且直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
, ![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在几何体ABDCE中,AB=AD,AE⊥平面ABD,M为线段BD的中点,MC∥AE,AE=MC.
(1)求证:平面BCD⊥平面CDE;
(2)若N为线段DE的中点,求证:平面AMN∥平面BEC.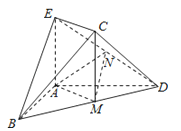
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂拟造一座平面为长方形,面积为![]() 的三级污水处理池.由于地形限制,长、宽都不能超过
的三级污水处理池.由于地形限制,长、宽都不能超过![]() ,处理池的高度一定.如果池的四周墙壁的造价为
,处理池的高度一定.如果池的四周墙壁的造价为![]() 元
元![]() ,中间两道隔墙的造价为
,中间两道隔墙的造价为![]() 元
元![]() ,池底的造价为
,池底的造价为![]() 元
元![]() ,则水池的长、宽分別为多少米时,污水池的造价最低?最低造价为多少元?
,则水池的长、宽分別为多少米时,污水池的造价最低?最低造价为多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是直线
是直线![]() 上任意一点,过
上任意一点,过![]() 作
作![]() ,线段
,线段![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() .
.
(Ⅰ)求点![]() 的轨迹
的轨迹![]() 对应的方程;
对应的方程;
(Ⅱ)过点![]() 的直线
的直线![]() 与点
与点![]() 的轨迹
的轨迹![]() 相交于
相交于![]() 两点,(
两点,( ![]() 点在
点在![]() 轴上方),点
轴上方),点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,且
,且![]() ,求
,求![]() 的外接圆的方程.
的外接圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的是一个几何体的直观图和三视图(其中正视图为直角梯形,俯视图为正方形,侧视图为直角三角形).
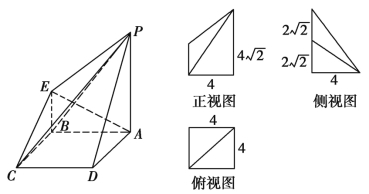
(1)求四棱锥P-ABCD的体积;
(2)若G为BC上的动点,求证:AE⊥PG.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】当今信息时代,众多高中生也配上了手机.某校为研究经常使用手机是否对学习成绩有影响,随机抽取高三年级50名理科生的一次数学周练成绩,用茎叶图表示如下图:
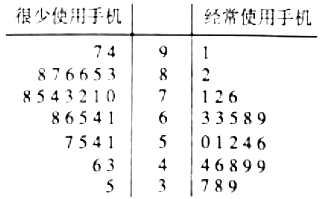
(1)根据茎叶图中的数据完成下面的![]() 列联表,并判断是否有95%的把握认为经常使用手机对学习成绩有影响?
列联表,并判断是否有95%的把握认为经常使用手机对学习成绩有影响?
及格( | 不及格 | 合计 | |
很少使用手机 | |||
经常使用手机 | |||
合计 |
(2)从50人中,选取一名很少使用手机的同学记为甲和一名经常使用手机的同学记为乙,解一道数列题,甲、乙独立解决此题的概率分别为![]() ,
, ![]() ,
, ![]() ,若
,若![]() ,则此二人适合结为学习上互帮互助的“师徒”,记
,则此二人适合结为学习上互帮互助的“师徒”,记![]() 为两人中解决此题的人数,若
为两人中解决此题的人数,若![]() ,问两人是否适合结为“师徒”?
,问两人是否适合结为“师徒”?
参考公式及数据: 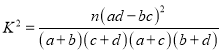 ,其中
,其中![]() .
.
| 0.10 | 0.05 | 0.025 |
| 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四棱锥P﹣ABCD的顶点P在底面ABCD上的投影恰好是A,其正视图与侧视图都是腰长为a的等腰直角三角形.则在四棱锥P﹣ABCD的任意两个顶点的连线中,互相垂直的异面直线共有 对.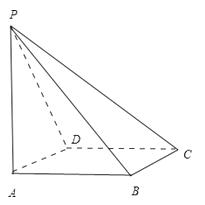
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com