已知函数f(x)=x2+2x,数列{an}的前n项和为Sn,对一切正整数n,点Pn(n,Sn)都在函数f(x)的图象上,且过点Pn(n,Sn)的切线的斜率为kn.
(1)求数列{an}的通项公式;(2)若bn=2kn•an,求数列{bn}的前n项和Tn.
解:(1)∵点P
n(n,S
n)都在函数f(x)=x
2+2x的图象上,
∴S
n=n
2+2n,(2分)
当n=1时,a
1=S
1=3;(3分)
当n≥2时,a
n=S
n-S
n-1=n
2+2n(n-1)
2-2(n-1)2n+1,(5分)
当n=1时,也满足,故a
n=2n+1.(6分)
(2)由f(x)=x
2+2x,求导可得f'(x)=2x+1,∵过点P
n(n,S
n)的切线的斜率为k
n
∴k
n=2n+2.
又∵b
n=2
kn•a
n,∴b
n=2
2n+2•(2n+1)=4(2n+1)•4
n.(8分)
∴T
n=4×3×4+4×5×4
2+4×7×4
3+…+4(2n+1)•4
n①
由①×④可得:4T
n=4×3×4
2+4×5×4
3+4×7×4
4+…+4(2n+1)•4
n+1②
①-②可得:-3T
n=4×[3×4+2•(4
2+4
3+…+4
n)-(2n+1)•4
n+1](10分)
=4×[3×4+2×
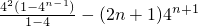
]∴T
n=
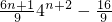
.(12分)
分析:(1)根据点在函数图象上,则点满足函数解析式,得到S
n的表达式,进而求得数列{a
n}的通项公式;
(2)根据题中条件求出k
n的表达式,结合(1)求得的数列{a
n}的通项公式,即可求得数列{b
n}的通项公式,进而可以利用错位相消法求出数列{b
n}的前n项和T
n.
点评:本题主要考查了数列的通项公式,以及利用错位相消法进行求和,属于中档题.

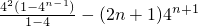 ]∴Tn=
]∴Tn=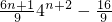 .(12分)
.(12分)

 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<