函数
为奇函数，该函数的部分图像如图所示，
、
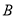分别为最高点与最低点，并且
，则该函数图象的一条对称轴为( )
A.
B.
C.
D.
科目：高中数学 来源：2013-2014学年湖北省黄冈市高三5月适应性考试理科数学试卷（解析版） 题型：填空题
1955年，印度数学家卡普耶卡（D.R.Kaprekar）研究了对四位自然数的一种交换：任给出四位数
，用的四个数字由大到小重新排列成一个四位数m，再减去它的反序数n(即将的四个数字由小到大排列，规定反序后若左边数字有0，则将0去掉运算，比如0001，计算时按1计算)，得出数
，然后继续对
重复上述变换，得数
，…，如此进行下去，卡普耶卡发现，无论是多大的四位数，只要四个数字不全相同，最多进行k次上述变换，就会出现变换前后相同的四位数t(这个数称为Kaprekar变换的核).通过研究10进制四位数2014可得Kaprekar变换的核为 .
查看答案和解析>>
科目：高中数学 来源：2013-2014学年湖北省黄冈市高三第二学期三月月考理科数学试卷（解析版） 题型：填空题
设
为不小于2的正整数，对任意
，若
（其中
，
，且
），则记
，如
，
.下列关于该映射
的命题中，正确的是.
①若
，
，则
②若，
，
，且
，则
③若，，
，
，且，
，则
④若，，，，且，，则
.
查看答案和解析>>
科目：高中数学 来源：2013-2014学年湖北省黄冈市高三第二学期三月月考文科数学试卷（解析版） 题型：解答题
已知函数
.
(1)当
时，求
的单调区间；
（2）若不等式
有解，求实数m的取值菹围；
（3）证明：当a=0时，
.
查看答案和解析>>
科目：高中数学 来源：2013-2014学年湖北省黄冈市高三第二学期三月月考文科数学试卷（解析版） 题型：填空题
在三棱锥
中，
，
平面ABC,
.若其主视图，俯视图如图所示，则其左视图的面积为
查看答案和解析>>
科目：高中数学 来源：2013-2014学年湖北省黄冈市高三第二学期三月月考文科数学试卷（解析版） 题型：选择题
下面几个命题中，假命题是（ ）
A.“若
,则
”的否命题；
B.“
，函数
在定义域内单调递增”的否定；
C.“
是函数
的一个周期”或“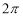
是函数
的一个周期”；
D.“
”是“
”的必要条件.
查看答案和解析>>
科目：高中数学 来源：2013-2014学年湖北省黄冈市高三下学期三月月考理科数学试卷（解析版） 题型：解答题
已知等比数列
的各项均为正数，且
成等差数列，
成等比数列.
（1）求数列的通项公式；
（2）已知
，记
，
,求证：
查看答案和解析>>
科目：高中数学 来源：2013-2014学年湖北省武汉市高三下学期4月调研测试文科数学试卷（解析版） 题型：填空题
在计算“1×2+2×3+...+n（n+1）”时，某同学学到了如下一种方法：
先改写第k项：k（k+1）=
由此得1×2-
.
.
.............
.
相加，得1×2+2×3+...+n（n+1）
.
类比上述方法，请你计算“1×2×3×4+2×3×4×+....+
”，
其结果是_________________.（结果写出关于
的一次因式的积的形式）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
为奇函数，所以
.所以函数可化为
.由
，设函数周期为T，可得
.所以
，所以函数的解析式为. 
.代入四个选项可得
是该函数图象的一条对称轴.
.若
，则
的取值范围是( )
B．
C．
D．