练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    15．若（2x+$\sqrt{3}$）100=a0+a1x+a2x2+…+a100x100，则（a0+a2+a4+…+a100）2-（a1+a3+a5+…+a99）2的值为（　　）
    A．1B．-1C．0D．2

    分析 用特殊值，令x=1，得出（2+$\sqrt{3}$）100=a0+a1+a2+…+a100，
    x=-1，得出（-2+$\sqrt{3}$）100=a0-a1+a2-…+a100，再因式分解，代入求值即可．

    解答 解：∵（2x+$\sqrt{3}$）100=a0+a1x+a2x2+…+a100x100，
    ∴当x=1时，（2+$\sqrt{3}$）100=a0+a1+a2+…+a100，
    当x=-1时，（-2+$\sqrt{3}$）100=a0-a1+a2-…+a100，
    ∴（a0+a2+a4+…+a100）2-（a1+a3+a5+…+a99）2
    =（a0+a1+a2+a3+a4+a5+…+a99+a100）（a0-a1+a2-a3+a4-a5+…-a99+a100）
    =（2+$\sqrt{3}$）100×（-2+$\sqrt{3}$）100
    =（-4+3）100
    =1．
    故选：A．

    点评 本题考查了二项式定理的应用问题，也考查了因式分解的应用问题，是基础题目．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    5．定义域为R的函数f（x）=$\left\{\begin{array}{l}{-2x（x≤0）}\\{f（x-1）（0＜x≤3）}\\{-3（x-4）^{2}+3（x＞3）}\end{array}\right.$，若函数g（x）=f（x）-2x-a有且只有两个零点，则实数a的取值范围为（　　）
    A．{a|-6≤a＜2}B．{a|-4≤a＜2}∪{-5}∪{-6}C．{a|-5≤a＜2}∪{-6}D．{a|-4≤a＜2}∪{-$\frac{14}{3}$}∪{-6}

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

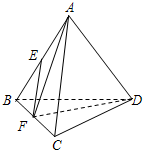
    6．在正四面体ABCD中，点E，F分别是AB，BC的中点，则下列结论错误的是（　　）
    A．异面直线AB与CD所成的角为90°B．直线AB与平面BCD成的角为60°
    C．直线EF∥平面ACDD．平面AFD垂直平面BCD

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    3．已知圆O：x2+y2=8，点A（2，0），动点M在圆上，则∠OMA的最大值为$\frac{π}{4}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

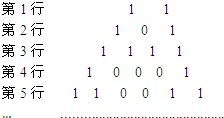    10．将杨辉三角中的奇数换成1，偶数换成0，得到如图所示的0-1三角数表、从上往下数，第1次全行的数都为1的是第1行，第2次全行的数都为1的是第3行，…，第n次全行的数都为1的是第2n-1行；第62行中1的个数是32．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    20．已知数列{an}满足a1=1，an+1=2an+1（n∈N+）
    （1）求a2，a3，a4，a5；
    （2）归纳猜想出通项公式an，并且用数学归纳法证明；
    （3）求证a100能被15整除．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．已知$tan（α+\frac{π}{5}）=2$，$tan（β-\frac{4π}{5}）=-3$，则tan（α-β）=（　　）
    A．1B．-$\frac{5}{7}$C．$\frac{5}{7}$D．-1

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    4．计算（1+i）（1-i）+（-1+i）=1+i．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．已知定义在实数集R的函数f（x）满足f（1）=4，且f（x）导函数f′（x）＜3，则不等式f（lnx）＞3lnx+1的解集为（　　）
    A．（1，+∞）B．（e，+∞）C．（0，1）D．（0，e）

    查看答案和解析>>

    同步练习册答案